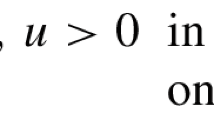Abstract
In this work, we investigate the following fractional \(p\)-Laplacian equation involving a concave-convex nonlinearities as follows, \({\rm (P_\lambda)} \begin{cases} (-\Delta)_p^s u = \lambda u^{q} + u^{r} &\mbox{in }\Omega, \\ u>0 & \text{in }\Omega, \\ u = 0 &\mbox{in }\mathbb{R}^N\setminus\Omega, \end{cases} \) where \(\Omega\subset\mathbb{R}^N\), \(N\geq 2\) is a bounded domain with \(C^{1,1}\) boundary \(\partial\Omega,\) \(\lambda >0\), \(1<p<\infty,\) \(s\in (0,1)\) such that \(N\geq s p,\) \(0<q<p-1<r\leq p^*_s-1,\) \(p^*_s = \frac{Np}{N-s p}\) is the fractional critical Sobolev exponent and the nonlinear nonlocal operator \((-\Delta)^s_p u\) with \(s\in (0,1)\) is the \(p\)-fractional Laplacian defined on smooth functions by \((-\Delta)^s_p u(x)=2 \underset{\epsilon\searrow 0}{\lim}\int_{\mathbb{R}^{N}\backslash B_\epsilon}\frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{|x-y|^{N+ ps}}\, dy,\qquad x\in \mathbb{R}^N. \) We use variational methods, in order to show the existence of multiple positive solutions to the problem \((P_\lambda)\) for different value of \(\lambda.\)
Similar content being viewed by others
References
D. Applebaum, Lévy Processes and Stochastic Calculus, Camb. Stud. Adv. Math. (Cambridge University Press, Cambridge, 2009), Vol. 116.
A. Cotsiolis and N. Tavoularis, “Best constants for Sobolev inequalities for higher order fractional derivatives,” J. Math. Anal. Appl. 295, 225–236 (2004).
D. Averna, S. Tersian, and E. Tornatore, “On the existence and multiplicity of solutions for Dirichlet’s problem for fractional equations,” Fract. Calc. Appl. Anal. 19 (1), 253–266 (2016).
B. Barrios, E. Coloradoc, R. Servadei, and F. Soriaa, “A critical fractional equation with concave-convex power nonlinearities,” Ann. Inst. H. Poincaré 32, 875–900 (2015).
G. Bonanno, R. Rodríguez-López, and S. Tersian, “Existence of solutions to boundary value problem for impulsive fractional differential equations,” Fract. Calc. Appl. Anal. 17 (3), 717–744 (2014).
B. Brandle, E. Colorado, A. de Pablo, and U. Sanchez, “A concave-convex elliptic problem involving the fractional Laplacian,” Proc. Roy. Soc. Edinburgh. Sec. A 143, 39–71 (2013).
A. Ghanmi and K. Saoudi, “The Nehari manifold for a singular elliptic equation involving the fractional Laplace operator,” Fractional Differential Calculus 6 (2), 201–217 (2016).
K. Saoudi, “A critical Fractional elliptic equation with singular nonlinearities,” Fractional Calculus and Applied Analysis 20 (6), 1507–1530 (2017).
A. Iannizzotto, S. Liu, K. Perera, and M. Squassina, “Existence results for fractional \(p\)-Laplacian problems via Morse theory,” Adv. Calc. Var. 9 (2), 101—125 (2016).
K. Perera, M. Squassina, and Y. Yang, “Bifurcation and multiplicity results for critical fractional \(p-\)Laplacian problems,” Mathematische Nachrichten 289, 332–342 (2016).
S. Mosconi, K. Perera, M. Squassina, and Y. Yang, “A Brezis Nirenberg result for the fractional \(p\)-Laplacian,” Calc. Var. 55, 105–130 (2016).
A. Ghanmi and K. Saoudi, “A multiplicity results for a singular problem involving the fractional \(p\)-Laplacian operator,” Complex. Var. Elliptic Equ. 61, 1199–1216 (2016).
A. Ambrosetti, H. Brezis, and G. Cerami, “Combined effects of concave and convex nonlinearities in some elliptic problems,” J. Funct. Anal. 122 (2), 519–543 (1994).
J. P. García Azorero and I. Peral Alonso, “Some results about the existence of a second positive solution in a quasilinear critical problem,” Indiana Univ. Math. J. 43, 941–957 (1994).
A. Ambrosetti, J. Garcia Azorero, and I. Peral, “Multiplicity results for some nonlinear elliptic equations,” J. Funct. Anal. 137 (1), 219—242 (1996).
Z. Guo and Z. Zhang, “\(W^{1,p}\) versus \(C^1\) local minimizers and multiplicity results for quasilinear elliptic equations,” J. Math. Anal. Appl. 2863, 32–50 (2003).
K. Saoudi, “Existence and non-existence of positive solutions for quasilinear elliptic problem,” Abstract and Applied Analysis Art. ID 275748, 9 pp (2012).
G. Tarantello, “On nonhomogeneous elliptic equations involving critical Sobolev exponent,” Ann. Inst. H. Poincaré, Anal. Non Linéaire 9, 281–304 (1992).
H. Brézis and E. Lieb, “A relations between pointwise convergence of functions and convergence of functionals,” Proc. Amer. Math. Soc. 88 (3), 486–490 (1983).
L. Brasco and G. Franzina, “Convexity properties of Dirichlet integrals and Picone-type inequalities,” Kodai Math. J. 37, 769–799 (2014).
D. G. de Figueiredo, J. P. Gossez, and P. Ubilla, “Local “superlinearity” and “sublinearity” for the \(p\)-Laplacian,” J. Funct. Anal. 257 (3), 721–752 (2009).
E. Lindgren and P. Lindqvist, “Fractional eigenvalues,” Calc. Var. Part. Diff. Equa. 49, 795—826 (2013).
K. Saoudi, “On vs. local minimizers for a critical functional related to fractional \(p\)-Laplacian,” Appl. Anal. 96 (9), 1586–1595 (2017).
E. Di Nezza, G. Palatucci, and E. Valdinoci, “Hitchhiker’s guide to the fractional Sobolev spaces,” Bull. Sci. Math. 136, 521–573 (2012).
N. Ghoussoub and D. Preiss, “A general mountain-pass principle for locating and classifying critical points,” Ann. Inst. H. Poincaré, Anal. Non Linéaire 6 (5), 321–330 (1989).
L. Brasco, E. Lindgren, and E. Parini, “The fractional Cheeger problem,” Interfaces and Free Boundaries 16 (2), 419–458 (2014).
A. Iannizzotto, S. Mosconi, and M. Squassina, “Global Hölder regularity for the fractional \(p\)-Laplacian,” Rev. Mat. Iberoam. 32, 1353–1392 (2016).
Acknowledgments
The authors wish to express gratitude to the referee for valuable remarks which contributed to the improvement of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Daoues, A., Hammami, A. & Saoudi, K. Multiplicity Results of a Nonlocal Problem Involving Concave-Convex Nonlinearities. Math Notes 109, 192–207 (2021). https://doi.org/10.1134/S0001434621010235
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0001434621010235