Abstract
In a simply connected bounded domain \(D\subset\mathbb C\) with rectifiable Jordan boundary \(\partial D\), we study the classes \(H_{2,\gamma}(D;\Omega_k,\Phi)\), \(k\in\mathbb N\), consisting of analytic functions \(f\in H_{2,\gamma}(D)\) in \(D\) each of which, for any \(t\in(0,1)\), satisfies the condition \(\Omega_k(f,t)\le\Phi(t)\). Here \(\Omega_k(f)\) is the generalized modulus of continuity of \(k\)th order in \(H_{2,\gamma}(D)\) and \(\Phi\) is a majorant. For these classes, we find upper and lower bounds for various \(n\)-widths, as well as upper bounds for the moduli of Fourier coefficients. We obtain a constraint on the majorant \(\Phi\) under which the exact values of these extremal characteristics can be calculated. In the case of the unit disk, similar results are obtained for classes of analytic functions whose definitions include the Hadamard compositions \(\mathscr D(\mathscr B_m,f)\) in addition to \(\Omega_k(f)\) and \(\Phi\). Concrete realizations of some obtained exact results are presented.
Similar content being viewed by others
References
V. M. Tikhomirov, “Approximation theory,” in Analysis – 2, Itogi Nauki i Tekhniki. Ser. Sovrem. Probl. Mat. Fund. Napr. (VINITI, Moscow, 1987), Vol. 14, pp. 103–260.
A. Pinkus, \(n\)-Widths in Approximation Theory (Springer- Verlag, Berlin, 1985).
S. D. Fisher, Function Theory on Planar Domains. A Second Course in Complex Analyses (John Wiley & Sons, New York, 2007).
Yu. A. Farkov, “On the best linear approximation of holomorphic functions,” J. Math. Sci. 218 (5), 678–698 (2016).
S. B. Vakarchuk and M. Sh. Shabozov, “The widths of classes of analytic functions in a disc,” Sb. Math. 201 (8), 1091–1110 (2010).
L. V. Taikov, “Diameters of certain classes of analytic functions,” Math. Notes 22 (2), 650–656 (1977).
N. Ainulloev and L. V. Taikov, “Best approximation in the sense of Kolmogorov of classes of functions analytic in the unit disc,” Math. Notes 40 (3), 699–705 (1986).
V. P. Zakharyuta and N. I. Skiba, “Estimates of \(n\)-diameters of some classes of functions analytic on Riemann surfaces,” Math. Notes 19 (6), 525–532 (1976).
M. Z. Dveirin, “Problems of best approximation of classes of functions analytic in the unit disk,” in Theory of Approximation of Functions (Nauka, Moscow, 1977), pp. 129–132 [in Russian].
O. G. Parfenov, “Widths of a class of analytic functions,” Math. USSR-Sb. 45 (2), 283–289 (1983).
Yu. A. Farkov, “Widths of Hardy classes and Bergman classes on the ball in \(\mathbb C^n\),” Russian Math. Surveys 45 (5), 229–231 (1990).
K. Yu. Osipenko and M. I. Stesin, “On widths of the Hardy class \(H_n\) in the \(n\)-dimensional ball,” Russian Math. Surveys 45 (5), 235–236 (1990).
S. B. Vakarchuk, “Exact values of widths of classes of analytic functions on the disk and best linear approximation methods,” Math. Notes 72 (5), 615–619 (2002).
S. B. Vakarchuk and V. I. Zabutnaya, “Best linear approximation methods for functions of Taikov classes in the Hardy spaces \(H_{q,\rho}\), \(q\ge1\), \(0<\rho\le1\),” Math. Notes 85 (3), 322–327 (2009).
M. Sh. Shabozov and G. A. Yusupov, “Best approximation methods and widths for some classes of functions in \(H_{q,\rho}\), \(1\le q\le\infty\), \(0<\rho\le1\),” Siberian Math. J. 57 (2), 369–376 (2016).
V. A. Abilov, F. V. Abilova, and M. K. Kerimov, “Sharp estimates for the rate of convergence of Fourier series of functions of a complex variable in the space
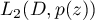 ,” Comput. Math. Math. Phys. 50 (6), 946–950 (2010).
,” Comput. Math. Math. Phys. 50 (6), 946–950 (2010).M. Sh. Shabozov and M. S. Saidusaynov, “Upper bounds for the approximation of certain classes of functions of a complex variable by Fourier series in the space \(L_2\) and n-widths,” Math. Notes 103 (4), 656–668 (2018).
Yu. I. Grigoryan, “Diameters of certain sets in function spaces,” Uspekhi Mat. Nauk 30 (3 (183)), 161–162 (1975).
S. G. Samko, A. A. Kilbas, and O. I. Marichev, Integrals and Derivatives of Fractional Order and Some of Their Applications (Nauka i Tekhnika and the technique, Minsk, 1987) [in Russian].
J. T. Scheik, “Polynomial approximation of the functions analytic in a disk,” Proc. Amer. Math. Soc. 17 (6), 1238–1243 (1966).
S. B. Vakarchuk, “On estimates in \(L_2(\mathbb{R})\) of mean \(\nu\)-widths of classes of functions defined via the generalized modulus of continuity of \(\omega_{\mathcal{M}}\),” Math. Notes 106 (2), 191–202 (2019).
S. B. Vakarchuk, “Approximation by classical orthogonal polynomials with weight in spaces \(L_{2,\gamma}(a,b)\) and widths of some functional classes,” Russian Math. (Iz. VUZ) 63 (12), 32–44 (2019).
D. Gaier, Lectures on the Theory of Approximation in the Complex Domain (Mir, Moscow, 1986) [in Russian].
A. I. Markushevich, Theory of Analytic Functions. Vol. II: Further Construction of the Theory (Nauka, Moscow, 1968) [in Russian].
P. K. Suetin, “Polynomials orthogonal over a region and Bieberbach polynomials,” Proc. Steklov Inst. Math. 100, 1–91 (1974).
T. Carleman, “Über die Approximation analytischer Funktionen durch lineare Aggregate von vorgegebenen Potenzen,” Ark. Mat. Astron. Fys. 17 (9), 1–30 (1923).
S. N. Mergelyan, “On completeness of systems of analytic functions,” Uspekhi Mat. Nauk 8 (4 (56)), 3–63 (1953).
V. I. Smirnov and N. A. Lebedev, Constructive Theory of Functions of a Complex Variable (Nauka, Moscow–Leningrad, 1964) [in Russian].
M. Keldych, “Sur l’approximation en moyenne par polynômes des fonctions d’une variable complexe,” Rec. Math. [Mat. Sbornik] N. S. 16(58) (1), 1–20 (1945).
V. L. Goncharov, Theory of Interpolation and Approximation of Functions (GITTL, Moscow, 1954) [in Russian].
V. M. Tikhomirov, Topics in Approximation Theory (Izd. Moskovsk. Univ., Moscow, 1976) [in Russian].
V. N. Temlyakov, Approximation of Periodic Functions (Nova Sci. Publ., Commack, NY, 1993).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vakarchuk, S.B. Estimates of the Values of \(n\)-Widths of Classes of Analytic Functions in the Weight Spaces \(H_{2,\gamma}(D)\). Math Notes 108, 775–790 (2020). https://doi.org/10.1134/S0001434620110218
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0001434620110218



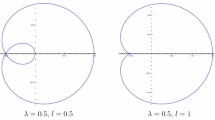
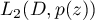 ,” Comput. Math. Math. Phys. 50 (6), 946–950 (2010).
,” Comput. Math. Math. Phys. 50 (6), 946–950 (2010).