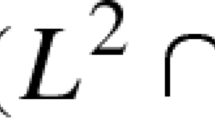Skip to main content
SpringerLink
Log in

Computational Experiments with Nilpotent Lie Algebras

  • Published:
Mathematical Notes Aims and scope Submit manuscript

Abstract

Results of computer experiments on the study of properties of generic Lie subalgebras with two generators in the Lie algebra of nilpotent matrices whose order does not exceed 10 are presented. The calculations carried out have made it possible to formulate several statements (so-called virtual theorems) on properties of the Lie subalgebras in question. The dimensions of the lower and upper central series and of the series of commutator subalgebras and the characteristic nilpotency property of the Lie subalgebras constructed here and of generic Lie subalgebras of codimension 1 in these Lie subalgebras are studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. Goze and Yu. Khakimjanov, Nilpotent Lie Algebras, in Math. Appl. (Kluwer Acad. Publ., Dordrecht, 1996), Vol. 361.

    Book  Google Scholar 

  2. GAP, http://www.gap-system.org.

  3. E. Luks, “What is the typical nilpotent Lie algebra?” in Computers in the Study of Non-Associative Rings and Algebras (Academic Press, New York, 1976), pp. 189–207.

    Google Scholar 

  4. R. Carles, “Sur la structure des algèbres de Lie rigides,” Ann. Inst. Fourier (Grenoble) 34 (3), 65–82 (1984).

    Article  MathSciNet  Google Scholar 

  5. N. Bourbaki, Lie Groups and Lie Algebras. Chap. 1–3. Lie Algebras, Free Lie Algebras, and Lie Groups, in Elements of Mathematics (Springer, Berlin, 1989; Mir, Moscow, 1976).

    MATH  Google Scholar 

  6. V. Gorbatsevich, Computational Experiments with Nilpotent Lie Algebra, arXiv: https://arxiv.org/abs/math.RA/1609.06493.

Download references

Acknowledgments

The author is grateful to the referee for a number of useful comments that have helped to present the experimental data obtained by the author more accurately.

Author information

Authors and Affiliations

  1. “Mathematical Notes,” Steklov Mathematical Institute of Russian Academy of Sciences, Moscow, 119991, Russia

    V. V. Gorbatsevich

Authors
  1. V. V. Gorbatsevich
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. V. Gorbatsevich.

Additional information

Russian Text © The Author(s), 2020, published in Matematicheskie Zametki, 2020, Vol. 107, No. 1, pp. 23–31.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gorbatsevich, V.V. Computational Experiments with Nilpotent Lie Algebras. Math Notes 107, 20–26 (2020). https://doi.org/10.1134/S0001434620010034

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0001434620010034

Keywords

Search

Navigation