Skip to main content
SpringerLink
Log in

Generalized Bezier transformation

  • Published:
Mathematical Notes Aims and scope Submit manuscript

Abstract

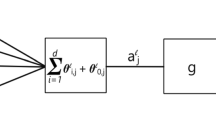
The properties of the generalized Bezier transformation and its application to the approximation of functions and the construction of curves are studied. The multidimensional version of this transformation is also considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. Chenin, M. Cosnard, F. Robert, Y. Robert, P. Witomski, and M. Tombs, Numerical Methods for CAD, translated from the French by M. Tombs (Kogan Page Ltd., London, 1985; Mir, Moscow, 1988).

  2. Yu. I. Volkov, “Certain positive linear operators,” Mat. Zametki 23(5), 659–669 (1978) [Math. Notes 23 (5–6), 363–368 (1978)].

    MATH  MathSciNet  Google Scholar 

  3. P.C. Sikkema and P. J. C. van der Meer, “The exact degree of local approximation by linear positive operators involving the modulus of continuity of the p-th derivative,” Indag. Math. 82(1), 63–76 (1979).

    Article  Google Scholar 

  4. Yu. I. Volkov, “Multidimensional approximation operators generated by Lebesgue-Stieltjes measures,” Izv. Akad. Nauk SSSR Ser. Mat. 47(3), 435–454 (1983) [Math. USSR-Izv. 22, 399–418 (1984)].

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Vinnichenko Kirovograd State Pedagogical University, Kirovograd, Ukraine

    Yu. I. Volkov

Authors
  1. Yu. I. Volkov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu. I. Volkov.

Additional information

Original Russian Text © Yu. I. Volkov, 2015, published in Matematicheskie Zametki, 2015, Vol. 97, No. 5, pp. 655–664.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Volkov, Y.I. Generalized Bezier transformation. Math Notes 97, 669–678 (2015). https://doi.org/10.1134/S0001434615050028

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0001434615050028

Keywords

Search

Navigation