Localization of nonlinear waves in elastic bodies with inclusions

Abstract

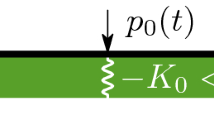
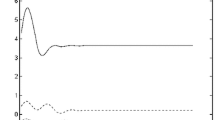
By the example of the problem of the motion of a semi-infinite string lying on an elastic base, a method for describing wave localization near inclusions is proposed for the case of a cubic nonlinearity of the base. The method applies the perturbation technique to the amplitude of a localized mode. The nature of the divergences is revealed, and the secular terms are found to belong to one of two types: inphase or antiphase with the localized wave. It is shown that a combination of the renormalization method and multiscale method provides a convergence of the solutions, which are sought for in the form of power series in the amplitude of the localized mode. It is found that the localization process is determined by the type of the discrete spectrum, type of the nonlinearity, and type of dispersion. The nonlinearity of the elastic base produces two characteristic effects. First, the frequency of the localized wave becomes dependent on the wave amplitude. Second, the system can generate traveling waves at multiple frequencies, which withdraw energy from the localized wave and cause it to decay. The decay behavior is determined by the minimum frequency of these traveling waves (because it must be higher than the cutoff frequency). The lifetime of the localized wave as a function of the mass of a dynamic inclusion exhibits a number of maxima. In particular, the first maximum corresponds to the minimum amplitude of the traveling wave at the triple frequency.