A refined measure of conditional maximum drawdown

Abstract

Risks associated to maximum drawdown have been recently formalized as the tail mean of the maximum drawdown distribution, called Conditional Expected Drawdown (CED). In fact, the special case of average maximum drawdown is widely used in the fund management industry also in association to performance management. It lacks relevant information on worst case scenarios over a fixed horizon. Formulating a refined version of CED, we are able to add this piece of information to the risk measurement of drawdown, and then get a risk measure for processes that preserves all the good properties of CED but following more prudential regulatory and management assessments, also in term of marginal risk contribution attributed to factors. As a special application, we consider the conditioning information given by the all time minimum of cumulative returns.

Introduction

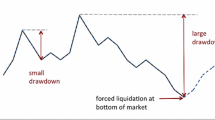
The current paper introduces and studies properties of a conditional refinement of CED which only considers maximal drawdown, but fails to reflect other worst scenarios within horizon, such that the all time minimum of a return path. The latter might have serious consequences for fund management where the CED is often applied. The problem is that two return paths may share the same maximum drawdown even though the all time minimum of one path is much higher than of the other, see Fig. 1.

Fig. 1

Running minimum and maximum drawdown of two simulated cumulative returns. Maximum drawdown remains the same, while running minimum increases (dotted line)

Thus the absolute risk, which also should be considered, is not fully captured by CED. With this aim in mind, we first propose a conditional path-dependent deviation risk measure, referred to as Co-CED, and defined as the conditional Average Value-at-Risk ($\text {AV@R}$) of a cumulative return process over a given investment period. Then, we specialize to the computation of Co-CED when conditioning on the minimum of the same return process.

The maximum drawdown of a financial time series (viz. cumulative returns) aims to the quantification of the relative drop of a given trading strategy’s value. In contrast to typical volatility measures such as the tracking error, here the whole time evolution of the time series over a fixed horizon is a crucial ingredient in the definition of the corresponding risk measure. When large drawdowns occur, measuring the risk only at the end of the investment horizon possibly underestimates potential liquidation issues, especially if losses exceed a threshold. Indeed, investors are naturally interested in the supremum and the infimum of stock prices, as well as in the maximum gain and the maximum loss over the horizon. This is because of market timing schemes involving the combination of purchases and short sales to ensure high gains. This obviously translates into the path behavior of cumulative returns. In the probabilistic terminology maximum loss means maximum drawdown, as a functional of the relevant path derived by the loss or drawdown process.¹ The tail conditional expectation of the maximum drawdown random variable is suggested, for example, by Chekhlov et al. (2005) in the context of portfolio optimization. One way to cope intra-horizon large losses is the maximum drawdown control strategy, see Grossman and Zhou (1993) for the case of an economy with only two securities, and Cvitanic and Karatzas (1995) for the case of several risky securities. An application to real estate is Hoesli and Hamelink (2004). More recent works are Pospisil and Vecer (2010) and Cherny and Obloj (2011). Outside the portfolio optimization realm, Magdon-Ismail and Atiya (2004) studied the link between the maximum drawdown and the mean return in the context of performance analysis. Vecer (2006) studied the expected maximum drawdown of a market in term of directional trading, for contracts which depend on the maximum drawdown. Insurance issues related to the maximum drawdown are treated in Carr et al. (2011), Vecer (2007) and Zhang et al. (2013), to cite a few.

Indeed, Goldberg and Mahmoud (2017) propose to apply the static $\text {AV@R}$ to the random variable modelling the maximum drawdown of cumulative returns, and get just CED. The basic idea is to resort to the definition of monetary risk measures for processes as developed in Cheridito et al. (2004), and then translate it into the definition of generalized path-dependent risk measure using the concept of generalized deviation measure by Rockafellar et al. (2006). Our first contribution is to extend this approach by considering the definition of static conditional risk measure, especially the conditional version of $\text {AV@R}.$ Admittedly, it is beyond the scope of the present paper to treat dynamic risk measures and their consistency properties. For a recent analysis which use a stochastic process in the domain of the coherent risk functional $\rho :\{0, \ldots ,T\} \times {\mathscr {D}} \times \varOmega \rightarrow \mathbb {R}$ see (Bielecki et al. 2014), where ${\mathscr {D}}$ is a set of adapted real-valued stochastic processes modelling cash flows. Instead, we argue that static conditional risk measures without consistency requirements might be justified by some literature on systemic risk measurement. Here we use a static conditional risk functional applied to processes, in order to handle maximum drawdown. On the other hand, (Föllmer 2019, Chap. 2) provided consistency properties of systemic risk measures. For a recent analysis of path-dependent risk and performance measures see (Kountzakis and Rossello 2020).

A second issue we study is the computation of our refined version of CED, when the conditioning is given by the running minimum of the same cumulative return’s path. While the theory and practice of drawdown is well developed, there is a small amount of academic contributions concerning the intra-horizon risk measured by the Value-at-Risk ($\text {V@R}$). Market risk measured by $\text {V@R}$ can be subject to underestimation, regardless the size of the probability of a loss, but rather due to the inability to capture diversification effects. In fact, the $\text {AV@R}$ has been proposed to improve on $\text {V@R}$ in the state space dimension, but still focusing on the expected loss at the end of the horizon. More recently, as already suggested by the Basel Committee on Banking Supervision in 1996 and subsequently in 2006 for for regulatory purposes, see Basel Committee on Banking Supervision (2006), some authors analyzed the consequences of considering also the magnitude of potential losses before the end of the horizon in the risk measurement process, see for example (Stulz 1996; Traynor 2005; Boudoukh et al. 2004; Rossello 2008; Bakshi and Panayotov 2010), and the more recent (Leippold and Vasiljević 2016). These authors analyze intra-horizon risk with $\text {V@R}$ applied to the random variable modelling the running minimum of cumulative returns over a fixed horizon, being able to capture jump or drift effects. In a marking-to-market environment, sudden losses may lead to margin calls or trigger rebalancing of the trading position during the holding period. Moreover, when trading strategies based on entry, exit or stop-loss levels, losses that exceed a specified level within the horizon bring more adverse events and eventually lead to counter-party risks. Hence intra-horizon risk measurement with running minimum is a relevant issue in a market-to-market world, because huge trading losses in short times may trigger margin calls and similar provisions. The recent market risk framework of the Basel Accords admits the $\text {AV@R}$ as an adequate risk measure because of its ability in providing sufficiently conservative risk estimates. As byproduct, Farkas et al. (2021) studied intra-horizon risk based on running minimum and $\text {AV@R}$ to better account for all extremes in a trading horizon since $\text {V@R}$ does not account for the whole magnitude of potential losses within it. Thus the literate on quantitative risk assessment devotes increasing interest in developing indices defined in term of the whole path of returns rather than point-in-time at the end of horizon.

The paper is organized as follows. Section 2 reviews the definitions of intra-horizon $\text {V@R}$ as a static risk measure for processes based on the running minimum. Thus, it recalls the definition of classical CED. Section 3 provides the new definition of conditional path-dependent risk measure for processes modelling cumulative returns. In Sect. 4 this definition leads to Co-CED, for which the axioms of a conditional path-dependent deviation measure are studied. Section 5 analyzes Co-CED of a portfolio and establishes the conditional marginal risk contributions. Sections 6 and 7 are devoted to computing Co-CED in the special case of conditioning given by the relevant event of a running minimum below the associated intra-horizon $\text {V@R}.$ A basic result is that Co-CED can correct underestimation suffered by classical CED. Section 8 presents an empirical analysis of Co-CED conditioned on the running minimum, using real world data. Section 9 concludes.

Review of unconditional path-dependent risks

For those processes $X=(X_t)_{t \in [0,T]}$ such that the pointwise infimum $\inf _{t \in [0,T]}X_t$ is measurable with respect to a fixed probability space $(\varOmega ,\mathscr {F},\mathsf {P}),$ the within-horizon Value-at-Risk risk is given by

$$\begin{aligned} \text {iV@R}_{\alpha }(X):=\text {V@R}_{\alpha }(\pi (X)), \quad \alpha \in (0,1), \end{aligned}$$

(1)

where the negative of the $\alpha$-quantile $\inf \left\{ x \in \mathbb {R}: \mathsf {P}(\pi (X) \leqslant x) \geqslant \alpha \right\}$ is the static $\text {V@R}$ of the running minimum $\pi (X)=\inf _{t \in [0,T]}X_t$ of X. Throughout the current paper we use the notation $\pi (X)$ to emphasize a functional acting on the paths of the underlying process, which provides the random variable relevant for our purpose. The risk measure for processes in (1) is an unconditional path-dependent risk measure based on forecasting the possible path of X over the whole investment horizon, whenever events of huge losses can occur. Some financial institutions use actively $\text {iV@R}$ for its ability to capture the time dimension of market risk: the quantile of the first-passage distribution over a fixed time horizon intrinsically provides the probability of incurring a loss at any point in time before and including the end of the given period. Indeed, the $\text {iV@R}$ risk measure resembles the ruin probability

$$\begin{aligned} \psi (c,T):= \mathsf {P}\left( c + \inf _{t \in [0,T]} X_t < 0 \right) =\mathsf {P}(\tau _c > T), \quad c \in \mathbb {R}, \end{aligned}$$

where $\tau _c:= \inf \{t \geqslant 0 : c + X_t < 0 \}$ is an hitting time of the process X. Taking the infimum $\inf _{c \in \mathbb {R}} \psi (c,T)$ in such a way the ruin probability is bounded above by the tail probability $\alpha \in (0,1)$ we get $\text {V@R}_{\alpha }\left( \inf _{t \in [0,T]} X_t \right)$, and whence $\psi$ is related to the first-passage probability for the process X. This yields a crucial piece of information in risk management for the survivorship of business. $\text {iV@R}$ is not a coherent path-dependent risk measure: $\pi$ is monotone but the one-time step $\text {V@R}$ is not subadditive, neither convex. From the perspective of portfolio management, it is the lack of convexity the main disadvantage for optimization problems. As a remedy for the lack of coherence, one might use instead the static $\text {AV@R}$ as suggested by Farkas et al. (2021).

The drawdown of X up to time $t \in [0,T]$ is $D^X_t:=M^X_t - X_t,$ i.e. the drop of X from its running maximum $M^X_t:=\sup _{u \in [0,t]} X_u.$ The maximum drawdown is the largest among all drawdowns over the whole investment horizon, thus now we have $\pi (X)=\sup _{t \in [0,T]} D^X_t.$ Be warned that the drawdown process $(D^X_t)_{t \in [0,T]}$ has not in general the same law of $(|X_t|)_{t \in [0,T]},$ that is the process reflected at zero. From the practitioners perspective, the maximum loss have to be disclosed by fund managers and investment advisors since they face drawdown limits in quantifying their investment strategies. Indeed, drawdown as a risk indicator is very popular in the hedge funds, where maximum drawdown adjusted measures such as the Calmar ratio are typically employed for performance measurement. In Goldberg and Mahmoud (2017), the conditional expected drawdown risk measure is for all X such that $\pi (X) \in L^{\infty }$ defined as

$$\begin{aligned} \text {CED}_{\alpha }(X):=\text {AV@R}_{1-\alpha }(\pi (X)), \quad \alpha \in (0,1), \end{aligned}$$

(2)

where the right-hand side in equation (2) is equal to the tail-mean

$$\begin{aligned} \tfrac{1}{1-\alpha } \int _{\alpha }^1 -\text {V@R}_c (\pi (X) ) \text {d}c \end{aligned}$$

of the probability distribution of the maximum drawdown random variable $\pi (X) \geqslant 0.$ By equation 1 and the nonnegativity of the maximum drawdown random variable, we have that the integrand above can be written

$$\begin{aligned} \inf \left\{ x \in \mathbb {R}: \mathsf {P}(\pi (X) > x ) \leqslant 1-\alpha \right\} . \end{aligned}$$

For example, if $\alpha =0.95$ then it is the average of the worst $(1-\alpha )\cdot 100\%$ drawdowns in the right tail of the probability distribution of $\sup _{t \in [0,T]} D^X_t.$ We can set $\text {CED}_1(X)=0,$ while $\text {CED}_0(X)=\mathsf {E}(\pi (X))$ is the average maximum drawdown. The path-transformation $\pi (X)$ given by the maximum drawdown is composed with the one-time step $\text {AV@R},$ and although the latter is a coherent risk measure for random variables it is well known that $\pi$ is not monotone. As a consequence, we can have $\text {CED}_{\alpha }(Y) \geqslant \text {CED}_{\alpha }(X)$ though $X \leqslant Y.$ Nevertheless, the conditional maximum drawdown satisfies all the properties of a generalized path-dependent risk measure, see Goldberg and Mahmoud (2017, Definition 3.1). In particular, $\text {CED}$ is always convex and degree-one positive homogeneous, hence is suitable as a tool for measuring path-dependent risk in association to portfolio’s contribution problems.

Remark 1

Albeit we adhere to the convention in Goldberg and Mahmoud (2017) and use the term path-dependent, this emphasis on processes rather than terminal returns can be misleading for certain audience dealing with dynamic risk measures or SPDEs, pricing and optimal exercising of American style options or even solving path-dependent PDEs.

Measuring conditional path-dependent risk

We are given a stochastic base $(\varOmega ,\mathscr {F}, (\mathscr {F}_t)_{t \in [0,T]}, \mathsf {P})$ satisfying the usual conditions, i.e., the probability space $(\varOmega ,\mathscr {F},\mathsf {P})$ is complete, the filtration $(\mathscr {F}_t)_{t \in [0,T]}$ is right-continuous, and the initial information $\mathscr {F}_0$ contains all the $\mathsf {P}$-null events of $\mathscr {F}.$ Here $T > 0$ is a non-random time representing the horizon. Almost surely (a.s.) random variables are identified as well as indistinguishable processes on the filtered space. Inequalities involving processes are meant as $X_t \leqslant Y_t$ $\mathsf {P}$-a.s. for all $0\leqslant t \leqslant T$ and so on. The process $X=(X_t)_{t \in [0,T]}$ models the cumulative returns over the whole investment horizon [0, T]. It can be picked from a subset ${\mathscr {S}} \subset {\mathscr {R}}^0$ of all $(\mathscr {F}_t)$-adapted càdlàg stochastic processes. For the risk measure we will develop later we choose ${\mathscr {S}}={\mathscr {R}}^1,$ the Banach space of $(\mathscr {F}_t)$-adapted càdlàg processes with norm

$$\begin{aligned} \Vert X\Vert _{{\mathscr {R}}^1}=\mathsf {E}\left( \sup _{t \in [0,T]}|X_t| \right) < \infty . \end{aligned}$$

Definition 1

Given a sub-sigma-algebra ${\mathscr {G}} \subset \mathscr {F}_T=\mathscr {F},$ a conditional path-dependent risk measure is a mapping $\rho (\,\cdot \, | \,{\mathscr {G}}): {\mathscr {R}}^1 \rightarrow L^1,$ with $L^1:=L^1(\varOmega ,{\mathscr {G}},\mathsf {P})$ modulo the equivalence classes of $\mathsf {P}$-a.s. equal random variables, given by the following composition

$$\begin{aligned} {\mathscr {R}}^1 \xrightarrow {\;\;\; \pi \;\;\;} L^1 \xrightarrow {\;\;\; {\tilde{\rho }} \;\;\;} L^1, \end{aligned}$$

where $\pi$ acts as a path-transformation, and ${\tilde{\rho }}$ is a conditional one-time step risk functional.

The interpretation is straightforward: One selects a random cumulative return X describing the possible paths of an investment strategy, hence the risk measurement is given in such a way all the information flow is encapsulated into the random variable $\pi (X),$ and finally a conditional risk measure is applied to incorporate some more observable information. Thus, the resulting quantification is random itself, and is affected by the conditioning information. In this sense, the above is a refinement of the definition of path-dependent risk measure given in Goldberg and Mahmoud (2017). Except for the codomain, Definition 1 can be considered as a restricted conditional version of risk measures for unbounded processes as studied in Cheridito et al. (2006), for the subspace ${\mathscr {R}}^1 \subset {\mathscr {R}}^0,$ where the latter (with the appropriate metric) is a complete but not locally convex space. The modelling choice based on ${\mathscr {R}}^1$ is not so reductive, since we can accommodate for stochastic models such as Brownian motion with drift, and some other Lévy (and in particular jump) processes.

Remark 2

We work with processes from the class ${\mathscr {R}}^1,$ thus the measurability of the pointwise supremum $\sup _{t \in [0,T]}|X_t|$ is guaranteed by definition. On the other hand, sine for every $x \in \mathbb {R}$ the event

$$\begin{aligned} \Big \{ \sup _{t \in [0,T]}|X_t| \leqslant x \Big \}=A^{*} \cup B^{*} \in \mathscr {F}\end{aligned}$$

is the disjoint union of the events

$$\begin{aligned} A^{*}:= \Big \{ \omega \in \varOmega : \,\sup _{t \in [0,T]}X_t(\omega ) \leqslant x,\; X_t(\omega ) \geqslant 0\;\text {for all}\, t \Big \} \end{aligned}$$

and

$$\begin{aligned} B^{*}:= \Big \{ \omega \in \varOmega : \,\sup _{t \in [0,T]}(-X_t(\omega )) \leqslant x,\; X_t(\omega ) < 0\;\text {for all}\, t \Big \}, \end{aligned}$$

we can deduce the measurability of the pointwise supremum $\sup _{t \in [0,T]}X_t$ for every process lying in ${\mathscr {R}}^1.$ A similar argument applies to the pointwise infimum. As a consequence, all the risk measures for processes described in the subsequent Sections are well defined. In particular, From the measurability of both $\sup _{t \in [0,T]}|X_t|$ and $\sup _{t \in [0,T]}X_t$ it follows the measurability of the maximum drawdown. Moreover, from the inequality

$$\begin{aligned} \Big | \sup _{t \in [0,T]}X_t \Big | \leqslant \sup _{t \in [0,T]}|X_t| \end{aligned}$$

together with the integrability of the latter random variable we also deduce that unconditional (also conditional, see Sect. 4) CED is well defined.

Refined version of CED

To introduce our variant of $\text {CED},$ first let us provide the following conditional version of a generalized path-dependent deviation measure.

Definition 2

A conditional path-dependent deviation measure with observable information structure ${\mathscr {G}} \subset {\mathscr {F}}_T:={\mathscr {F}},$ is a conditional path-dependent risk measure $\rho ( \,\cdot \, | \,{\mathscr {G}}) : {\mathscr {R}}^1 \rightarrow L^1$ satisfying the following properties:

• (C1) Normalization: $\rho (C \, | \,{\mathscr {G}})=0,$ for all constant path $C \in {\mathscr {S}}.$

• (C2) Positivity: $\rho (X \, | \,{\mathscr {G}}) \geqslant 0,$ for all $X \in {\mathscr {S}}.$

• (C3) Conditional shift invariance: $\rho (X + C \, | \,{\mathscr {G}})=\rho (X \, | \,{\mathscr {G}}),$ for all $X \in {\mathscr {S}}$ and all $\mathsf {P}$-a.s. constant path $C \in {\mathscr {S}}.$

• (C4) Convexity: $\rho (\lambda X + (1- \lambda ) Y \, | \,{\mathscr {G}}) \leqslant \lambda \rho (X\, | \,{\mathscr {G}}) + (1-\lambda )\rho (Y \, | \,{\mathscr {G}}),$ for all $X,Y \in {\mathscr {S}}$ and all $\lambda \in [0,1].$

• (C5) Positive homogeneity: $\rho (\lambda X \, | \,{\mathscr {G}})=\lambda \rho ( X \, | \,{\mathscr {G}}),$ for all $X \in {\mathscr {S}}$ and $\lambda >0.$

From now on, we write $\pi _1(X)$ for the maximum drawdown of X over the appropriate horizon, and $\pi _2(X)$ for the running minimum over the same horizon. Next, we give the new definition of $\text {CED},$ namely co-$\text {CED}:$

Definition 3

(Co-CED) Given a random path $X \in {\mathscr {S}}$ over a fixed time horizon $T \in (0, \infty ),$ the refined $\text {CED}$ risk measure dependent on the information structure ${\mathscr {G}}$ is the mapping $\text {CED}_{\alpha }( \,\cdot \, | \,{\mathscr {G}}) : {\mathscr {R}}^1 \rightarrow L^1$ given by

$$\begin{aligned} \text {CED}_{\alpha }(X \, | \,{\mathscr {G}}):= \tfrac{1}{1-\alpha } \int _{\alpha }^1 -\text {V@R}_c (\pi _1(X) \, | \,{\mathscr {G}}) \text {d}c, \quad \alpha \in (0,1). \end{aligned}$$

(3)

This version is law invariant, because $\text {CED}_{\alpha }$ is essentially applied to the conditional distribution of $\pi _1(X)$ given ${\mathscr {G}},$ i.e. $\mathsf {P}_{\pi _1(X) \, | \,{\mathscr {G}}}.$ Observe that $\text {V@R}$ inside the tail-mean is in conditional form, i.e. is the $\text {V@R}$ of $\pi _1(X)$ conditional on the information induced by ${\mathscr {G}}.$ Thus $\text {CED}_{\alpha }(X \, | \,{\mathscr {G}})$ is nothing but $\text {AV@R}_{1-\alpha }(\pi _1(C) \, | \,{\mathscr {G}}).$ This representation is based on the notion of conditional quantile, which can be defined using regular conditional probability and the corresponding conditional distribution function (see Acciaio and Goldammer 2013 and Acciaio and Penner 2011), or alternatively using the notions of ${\mathscr {G}}$-upper envelope of a random variable and of adjusted indicator function (see Hirz 2015). In the current setting, we refer to these approaches but assuming a constant deterministic $\alpha \in (0,1).$ We see that co-$\text {CED}$ is indeed a conditional path-dependent deviation measure.

Lemma 1

(Properties of Co-CED) For all cumulative returns $X,Y \in {\mathscr {S}}$ and all $\mathsf {P}$-a.s. constant paths $C \in {\mathscr {S}},$ the co-$\text {CED}$ risk measure satisfies properties (C1)–(C5) of Definition 2, for every $\alpha \in (0,1).$

Proof

Set $\rho (C \, | \,{\mathscr {G}})=\text {AV@R}_{1-\alpha }(\pi _1(C) \, | \,{\mathscr {G}}).$ The maximum drawdown of a path $C \in {\mathscr {S}}$ of constant deterministic value is always zero, $\pi _1(C)=0.$ Thus, $\rho (C \, | \,{\mathscr {G}})=\text {AV@R}_{1-\alpha }(0 \, | \,{\mathscr {G}})=0$ regardless the tail probability $\alpha \in (0,1),$ and (C1) is satisfied. Because the maximum drawdown random variable $\pi _1(X)$ is by definition non-negative for any $\omega \in \varOmega ,$ then condition (C2) is fulfilled due to the monotonicity of the conditional $\text {AV@R}$ (see Pflug and Römisch (2007), Proposition 2.57, (iv)). By combining the convexity of the path-transformation given by the maximum drawdown (see (Goldberg and Mahmoud (2017), Proposition 3.3) with the convexity of the conditional $\text {AV@R}$ (see, after a change in sign, Pflug and Römisch (2007), Proposition 2.57, (ii)), also condition (C4) is satisfied. To verify condition (C3), we observe that by the shift invariance of the maximum drawdown (see Goldberg and Mahmoud (2017, Lemma 3.2) $\text {AV@R}_{1-\alpha }(\pi _1(X+C) \, | \,{\mathscr {G}})$ equals $\text {AV@R}_{1-\alpha }(\pi _1(X) \, | \,{\mathscr {G}}),$ then $\rho (X + C \, | \,{\mathscr {G}}) =\rho (X \, | \,{\mathscr {G}}).$ Finally, since the maximum drawdown is positive homogeneous (see the proof of Goldberg and Mahmoud (2017, Proposition 3.5) as well as the conditional $\text {AV@R}$ (see Pflug and Römisch (2007), Proposition 2.57, (iii)) when $\varLambda =\lambda >0$ is just a positive constant) we have that $\rho (\lambda X \, | \,{\mathscr {G}})$ is equal to $\lambda \rho (X \, | \,{\mathscr {G}}),$ for any $\lambda >0$ and condition (C5) is satisfied. $\square$

Remark 3

We treat random paths X belonging to the larger class ${\mathscr {R}}^1 \supset {\mathscr {R}}^{\infty },$ to account for not necessarily bounded càdlàg processes. On the other hand, if we choose ${\mathscr {G}}=\{\varnothing , \varOmega \}$ then we obtain the unconditional $\text {CED}$ now defined on ${\mathscr {R}}^1.$

Our interest in the co-$\text {CED}$ is due to the possible specification of (3) when the information structure ${\mathscr {G}}$ is the stress scenario induced by ${\mathscr {G}}:= \sigma (\pi _2(X)) \subset \mathscr {F},$ i.e. it is represented by conditioning on the running minimum. The joint treatment of the worst case scenario associated to the running minimum, and the percentage/volatility risk associated to the maximum drawdown is relevant from the management point of view. Hence, using $\text {CED}_{\alpha }(X \, | \,\sigma (\pi _2(X)))$ we try to predict the risk associated to the maximum drawdown of a portfolio, given specific economic conditions on its worst behavior within the horizon (see Sect. 6).

Remark 4

Observe that the running minimum of $C \in {\mathscr {S}}$ is just C. When in condition (C3) co-$\text {CED}$ given by equation (3) is specified through $\sigma (\pi _2(X))$ we have that $\text {CED}_{\alpha }(X+C \, | \,\sigma (\pi _2(X)))$ is equal to $\text {CED}_{\alpha }(X\, | \,\sigma (\pi _2(X+C))).$ We also note that the events $\{\pi _2(X) \in B\}$ and $\{\pi _2(X+C) \in B\}=\{\pi _2(X)+C \in B\}$ are in general different for any Borel set $B \subset \mathbb {R},$ thus the conditional maximum drawdown risk measure retains the path modification, in the sense that deterministically shifting the path X up or down left the maximum drawdown unchanged while might increase (decrease) the running minimum for positive (negative) C. In condition (C5) we have $\pi _2(\lambda X)=\lambda \pi _2(X).$

Conditional Euler allocation

The analysis of portfolio risk through marginal risk contributions is well developed, and when integrated with drawdown risk measurement enable us to estimate the impact of a trade to the overall portfolio’s drawdown risk. Let $P=(P_t)_{t \in [0,T]}$ be the cumulative portfolio return over the horizon, whit time-t value $P_t=\sum _{i=1}^n w_i R_{i,t},$ and constant weight $w_i$ attributed to the i-th asset’s return $R_i=(R_{i,t})_{t \in [0,T]} \in {\mathscr {S}}$ over the same period, for a fixed number $n \in \mathbb {N}$ of assets. It is possible to extend the definition of marginal risk contribution to the current conditional framework, and then to conceive the change rate of the co-dependent maximum drawdown risk measure when the holding $w_i$ of the portfolio is increased or decreased within the horizon. Observe that the convex combination defining the path of portfolio return belongs to ${\mathscr {S}}$ too. Afterwards we write $-\text {V@R}_c (\cdot \, | \,{\mathscr {G}})=q_{{\mathscr {G}},c}(\cdot ).$

Lemma 2

The conditional marginal risk contribution of $R_i \in {\mathscr {S}}$ to the overall portfolio $P \in {\mathscr {S}}$ over [0, T] is given by

$$\begin{aligned} \text {MRC}_i(P \, | \,{\mathscr {G}})=\frac{\partial \text {CED}_{\alpha }(P \, | \,{\mathscr {G}})}{\partial w_i},\quad \mathsf {P}\text {-a.s.} \end{aligned}$$

(4)

given the information structure ${\mathscr {G}} \subset \mathscr {F},$ and for all $\alpha \in (0,1),$ provided that $\pi _1(P), \pi _1(P + \varepsilon _k R_i),$ for $k \in \mathbb {N}$ and $i=1,\ldots ,n,$ have $\mathsf {P}$-a.s. finite conditional $\text {AV@R},$ for a suitable sequence $(\varepsilon _k)_{k \in \mathbb {N}}$ of ${\mathscr {G}}$-measurable real-valued random variables converging to zero $\mathsf {P}$-a.s., and in addition requiring that

$$\begin{aligned} \mathsf {P}\big (\pi _1(P) \leqslant q_{{\mathscr {G}},c}(\pi _1(P)) \, | \,{\mathscr {G}} \big )=\alpha , \quad \mathsf {P}\text {-a.s.} \end{aligned}$$

while $\pi _1(P)$ is $\mathsf {P}$-a.s. constant over the event $\big \{\pi _1(P) = q_{{\mathscr {G}},c}(\pi _1(P))\big \}.$

Proof

Let $\text {CED}_{\alpha }(P \, | \,{\mathscr {G}})=\text {AV@R}_{1-\alpha }(\pi _1(P) \, | \,{\mathscr {G}}),$ and recall representation (3). By Definition 7.3 of Hirz (2015), the conditional $\text {AV@R}$ of a portfolio P is a special case of the weighted conditional $\text {AV@R}$ of the same portfolio. Thus, (Hirz 2015, Lemma 7.7(l)) applies and we have that co-$\text {CED}$ contributions of $R_i$ to the portfolio cumulative return P is given by the directional derivative

$$\begin{aligned} \text {CED}_{\alpha }(P,R_i \, | \,{\mathscr {G}}) = \lim _{k \rightarrow \infty } \frac{\text {CED}_{\alpha }(P + \varepsilon _k R_i \, | \,{\mathscr {G}})}{\varepsilon _k} \quad \text {in}\;L^1, \end{aligned}$$

for every sequence $(\varepsilon _k)_{k \in \mathbb {N}}$ of ${\mathscr {G}}$-measurable real-valued random variables converging to zero $\mathsf {P}$-a.s., and such that $\mathsf {P}(\cup _k \{\varepsilon _k =0\})=0.$ Now, by portfolio translation invariance, (Hirz 2015, Lemma 7.7(d)), and conditional translation invariance, (Hirz 2015, Lemma 7.7(f)), and by defining $\text {MRC}_i(P \, | \,{\mathscr {G}}):=\text {CED}_{\alpha }(P,R_i \, | \,{\mathscr {G}})$ we are done. $\square$

The proof of Lemma 2 is an application of the results for spatial conditional risk measures in Hirz (2015), and similar results apply to conditional dynamic risk measures in Acciaio and Goldammer (2013), Acciaio and Penner (2011) and Filipović et al. (2012). In particular they are proved in Hoffmann et al. (2016) from the perspective of systemic risk measurement (see also Sect. 6). Due to positive homogeneity (C5) of Definition 2, together with Lemma 2 and Corollary 7.8 of Hirz (2015), we have that the overall portfolio conditional drawdown risk can be decomposed as:

$$\begin{aligned} \sum _{i=1}^n w_i \text {MRC}_i(P \, | \,{\mathscr {G}}) = \text {CED}_{\alpha }(P \, | \,{\mathscr {G}}), \quad \mathsf {P}\text {-a.s.} \end{aligned}$$

This is the conditional Euler’s principle of allocating coherently the risk induced by portfolio’s components to the overall portfolio.

Application of Co-CED

Nowadays, there exists an extensive literature on systemic risk centered on the conditional versions of basic risk measures such as $\text {V@R}$ and $\text {AV@R}.$ In fact, the starting point of this body of research is the notion of CoVaR which stands for conditional Value-at-Risk. The idea behind CoVaR is to use the conditional distribution of a random variable (representing a particular financial institution) given that another random variable (representing a different institution) is in stress. Also, the conditional Expected Shortfall, CoES for short, is nothing but the $\text {AV@R}$ of the first random variable conditional on the second, and can be represented as the tail-mean of the former given the CoVaR of the latter. In the path-dependent setting the definition of CoES for a portfolio process $P \in {\mathscr {S}}$ is a specification of Definition 3, i.e. when $\text {CED}_{\alpha }(P \, | \,\sigma (\pi _2(P)))$ is evaluated at the event $A_{\beta }=\{\pi _2(P) \leqslant \text {iV@R}_{\beta }(P) \}$ for $\beta \in (0,1).$ Assuming from now on that both the running minimum and the maximum drawdown have continuous marginals, we then can write:

$$\begin{aligned} \text {CED}_{\alpha }(P \, | \,A_{\beta }) = \mathsf {E}\left( \pi _1(P) \, | \,\pi _1(P) > q_{A_{\beta },\alpha }(\pi _1(P)), A_{\beta } \right) , \quad \text {for all} \quad \alpha , \beta \in (0,1), \end{aligned}$$

(5)

where $q_{A_{\beta },\alpha }(\pi _1(P))$ is the conditional quantile of the portfolio maximum drawdown’s distribution $F_{\pi _1(P) \, | \,A_{\beta }}.$ The structure of this conditional path-dependent risk measure rests as in the unconditional case in Goldberg and Mahmoud (2017) on characterizing certain thresholds that possible losses may exceed. In the current settings crucial levels concern the running minimum and the maximum drawdown together, where (in contrast to the reasoning developed in the systemic risk literature) the former is not the system and the latter is not a part of it. Instead they are embodied in the same random mechanism distilled by the path-dependency considered over the horizon. The main result of this section is the following:

Proposition 1

Let assume that $\pi _2(P) \leqslant \pi _1(P),$ for $\pi _1(P),\pi _2(P) \in L^1.$ Moreover, assume the same notation as in equation (5). Then, there exist versions of $\pi _1(P),\pi _2(P)$ having the same distributions with corresponding portfolio ${\tilde{P}}$ such that

$$\begin{aligned} \text {CED}_{\alpha }\left( {\tilde{P}}\right) \leqslant \text {CED}_{\alpha }\left( {\tilde{P}} \, | \,A_{\beta }\right) , \quad \text {for all} \quad \alpha , \beta \in (0,1). \end{aligned}$$

Proposition 1 says that unconditional $\text {CED}_{\alpha }$ underestimates the path-dependent risk associated to a portfolio ${\tilde{P}},$ unless one considers the additional information on a worst case scenario induced by the all time minimum of ${\tilde{P}}$ based on a second probability threshold $\beta .$ But this is true only if the effect of a worst case scenario due to the running minimum of cumulative returns is smaller than the maximum drawdown. Empirically, this effect comes into play whenever we restrict the estimation of unconditional and conditional $\text {CED}$ to those portfolio’s cumulative returns for which the minimum is less than the corresponding maximum drawdown, over a fixed time window. Under this restriction is possible that an increase in the magnitude of the minimum entails an almost unchanged maximum drawdown, and as a consequence the risk measurement of the latter becomes more informative provided that we add the information on the worst case scenario concerning the former. To prove Proposition 1, we essentially use results on stochastic orders and the corresponding comparison arguments studied in Sordo et al. (2018).

Proof

1 By assumption $\pi _2(P) \leqslant \pi _1(P),$ then there exist two versions ${\overline{D}} {\mathop {=}\limits ^{\text {d}}}\pi _1(P)$ and ${\underline{X}}{\mathop {=}\limits ^{\text {d}}}\pi _2(P)$ such that ${\underline{X}} \leqslant _{\text {st}}{\overline{D}}$ in the usual stochastic order, i.e. $F_{{\underline{X}}}(t) \geqslant F_{{\overline{D}}}(t)$ for all reals t. But $\leqslant _{\text {st}}$ implies $\leqslant _{\text {icx}},$ the increasing convex order, see Definition 1.5.1(ii) in Müller and Stoyan (2002). Thus, by Corollary 1.5.21 of Müller and Stoyan (2002), there exist random variables $W {\mathop {=}\limits ^{\text {d}}}{\underline{X}}$ and $Z {\mathop {=}\limits ^{\text {d}}}{\overline{D}}$ such that the conditional random variable $\{Z \, | \,W= t\}$ is stochastically increasing in t,  i.e.

$$\begin{aligned} \{Z \, | \,W= s\} \leqslant _{\text {st}}\{Z \, | \,W= t\} \quad \text {for all reals} \quad s \leqslant t. \end{aligned}$$

We are in position to apply Theorem 12 in Sordo et al. (2018), by identifying $\text {CED}_{\alpha }\left( {\tilde{P}}\right)$ with $\text {CoES}_{\alpha ,\alpha }\left( Z \, | \,Z \right)$ and $\text {CED}_{\alpha }\left( {\tilde{P}} \, | \,A_{\beta }\right)$ with $\text {CoES}_{\alpha ,\beta }\left( Z \, | \,W \right) .$ Assume without loss of generality that $x \leqslant y,$ for reals x, y. The last condition required by Sordo et al. (2018, Theorem 12) that the copula

$$\begin{aligned} C(u,v)=\mathsf {P}\left( Z \leqslant x, Z \leqslant y \right) =\mathsf {P}(Z \leqslant x)=F_Z(x) \end{aligned}$$

is smaller than the copula

$$\begin{aligned} C'(u,v)=\mathsf {P}\left( Z \leqslant x, W \leqslant y \right) =F_{W,Z}(x,y), \end{aligned}$$

for all $u,v \in (0,1),$ written $C \prec C',$ is easily verified, just observe that

$$\begin{aligned} \mathsf {P}(W \leqslant y)=F_W(y) \geqslant F_W(x) \geqslant F_Z(x), \end{aligned}$$

also that $F_W(y) \geqslant F_Z(y),$ and any copula function is increasing in both variables. Coming back to the original versions of all the involved random variables, (Sordo et al. 2018, Theorem 12) entails the desired result. $\square$

Application of conditional Euler allocations

It is well known that whatever the framework is (static, path-dependent, dynamic) portfolio risk is never the weighted sum of individual risk contributions. The tool of risk contribution as employed for management or allocation purposes enable us to measure the approximate change in portfolio risk, when increasing the individual exposure by a small amount while keeping the remaining exposures fixed. Under the assumption of continuous marginal distributions for the running minimum and the maximum drawdown, we resort to representation (5) given in Sect. 6 and set

$$\begin{aligned} B=\left\{ \pi _1(P) > q_{A_{\beta }\alpha }(\pi _1(P))\right\} , \end{aligned}$$

to give a special application of Lemma 2 by assuming, additionally, that $\sigma (\pi _2(P)) \subset {\mathscr {G}}.$ Thus we have:

Lemma 3

Let’s assume that $\mathsf {P}(A_{\beta } \cap B) >0.$ For a cumulative portfolio return $P \in {\mathscr {S}}$ with strictly positive maximum drawdown, $\pi _1(P) >0,$ and two random times $\tau _1 < \tau _2 \leqslant T$ such that

$$\begin{aligned} \pi _1(P)= P_{\tau _2} - P_{\tau _1}=\sum _{i=1}^n w_i R_{i, \tau _2} - \sum _{i=1}^n w_i R_{i, \tau _1}, \end{aligned}$$

the marginal risk contribution of $R_i \in {\mathscr {S}}$ given the portfolio’s intra-horizon $\text {V@R}$ at the level $\beta \in (0,1)$ is

$$\begin{aligned} \text {MRC}_i(P \, | \,A_{\beta })= \mathsf {E}\big ( R_{i, \tau _2} - R_{i, \tau _1} \, | \,A_{\beta } \cap B \big ) =\text {CED}_{\alpha }(R_i \, | \,A_{\beta }), \end{aligned}$$

(6)

for a level $\alpha \in (0,1)$ of the co-$\text {CED}$ of the i-th security’s cumulative return.

Proof

The conditional $\text {CED}$ of the portfolio P at level $\alpha$ can be written

$$\begin{aligned} \text {CED}_{\alpha }(P \, | \,A_{\beta })= & {} \mathsf {E}\left( \pi _1(P) \, | \,A_{\beta } \cap B \right) \\= & {} \frac{\mathsf {E}\left( \pi _1(P) \mathbf {I}_{A_{\beta } \cap B} \right) }{\mathsf {P}(A_{\beta } \cap B)}. \end{aligned}$$

We get the following chain of equivalences

$$\begin{aligned} \frac{\partial \text {CED}_{\alpha }(P \, | \,A_{\beta })}{\partial w_i}= & {} \frac{\partial }{\partial w_i} \frac{\mathsf {E}\left( \pi _1(P) \mathbf {I}_{A_{\beta } \cap B} \right) }{\mathsf {P}(A_{\beta } \cap B)}\\= & {} \frac{\partial }{\partial w_i} \frac{\mathsf {E}\left( (P_{\tau _2} - P_{\tau _1}) \mathbf {I}_{A_{\beta } \cap B} \right) }{\mathsf {P}(A_{\beta } \cap B)}\\= & {} \frac{\mathsf {E}\left( \tfrac{\partial }{\partial w_i} \sum _{i=1}^n w_i \left( R_{i, \tau _2} - R_{i, \tau _1} \right) \mathbf {I}_{A_{\beta } \cap B} \right) }{\mathsf {P}(A_{\beta } \cap B)} \\= & {} \frac{\mathsf {E}\left( \left( R_{i, \tau _2} - R_{i, \tau _1} \right) \mathbf {I}_{A_{\beta } \cap B} \right) }{\mathsf {P}(A_{\beta } \cap B)}\\= & {} \mathsf {E}\left( R_{i, \tau _2} - R_{i, \tau _1} \, | \,A_{\beta } \cap B \right) \\= & {} \text {CED}_{\alpha }( R_i \, | \,A_{\beta }), \end{aligned}$$

where in the last line we used $R_{i, \tau _2} - R_{i, \tau _1}=\pi _1(R_i),$ thus obtaining the desired result. $\square$

More important, under the hypotheses of a running minimum observable in the i-th risk factor being smaller than the corresponding maximum drawdown, $\pi _2(R_i) \leqslant \pi _1(R_i),$ an application of Proposition 1 reveals the potential underestimation issue also for the marginal risk contributions: since

$$\begin{aligned} \text {MRC}_i(P)=\text {CED}_{\alpha }(R_i)\leqslant \text {CED}_{\alpha }( R_i \, | \,A_{\beta })= \text {MRC}_i(P \, | \,A_{\beta }), \end{aligned}$$

our refined version should recover the problem by adding more information on the worst case scenarios over the horizon, with respect to the unconditional one. If $\pi _2(R_i) \leqslant \pi _1(R_i)$ is true only for some outcomes, one can turn to versions ${\tilde{P}},{\tilde{R}}_i$ of the portfolio and the corresponding i-th risk factor.

Empirical comparison: CED Vs Co-CED

In this Section we essentially try to test the claim of Proposition 1. We propose using an atypical dataset comprising four cryptocurrencies, namely Bitcoin, Ethereum, XRP and Stellar which are the best in term of market capitalization. This should be considered as an “emerging market” with very high volatility. We use a total of $1558 \times 4$ data points for the daily time series starting from February 23, 2017 to May 30, 2021. In addition, we form a fixed equally weighted portfolio (no-leverage, long) assuming no transaction costs or market frictions. The summary statistics of the four indices together with the portfolio are listed in Table 1. Observe that all the securities are asymmetrically distributed, also with different magnitude and sign of skewness and kurtosis. On the other hand, their portfolio has a “more normal” empirical distribution.

Table 1 Summary statistics of daily Returns

Fig. 2

Historical returns of Bitcoin

Fig. 3

Historical returns of Ethereum

Fig. 4

Historical returns of XRP

Fig. 5

Historical returns of Stellar

A check of the cryptocurrencies’ plots in Figs. 2, 3, 4, and 5 suggests that extreme negative returns can affect higher positive changes as represented by maximum drawdowns, especially for the first three time series. We transform the original portfolio’s return series into a cumulative return series. On the latter we perform a historical simulation of running minimums and maximum drawdowns, using a 5-days moving window: we scroll down the portfolio’s cumulative return series one day per time keeping fixed the length of five data points. The resulting pair of empirical distributions has now $1553 \times 2$ data points. Further, we need to extract a sub-sample corresponding to the condition stated in Proposition 1, that the distribution of the running minimum random variable contains values smaller than those of the maximum drawdown distribution. We point out how this is the main limitation of our suggested estimation procedure. To implement our refined risk measure, we derive two empirical distributions of maximum drawdown conditioned on the simulated values of the running minimum being less than or equal to the plug-in estimators of the corresponding $\text {V@R}_{0.01}$ and $\text {V@R}_{0.05},$ respectively. Then, we compute four plug-in estimators of the $\text {AV@R}_{0.01}$ and $\text {AV@R}_{0.05}$ of the empirical conditional distribution of the maximum drawdown. These represent non-parametric estimates of $\text {CED}_{\alpha }( {\tilde{P}} \, | \,A_{\beta })$ for possible combination of probability thresholds $\alpha =0.99,0.95$ and $\beta =0.01,0.05,$ respectively. The results are summarized in Table 2, where they are compared with two non-parametric estimates of $\text {CED}_{\alpha }( {\tilde{P}}).$

Table 2 Point estimators of Co-CED and CED

The empirical test confirm the possible underestimation of CED with respect to Co-CED. Repeating the above calculations for different portfolio weights does not alter so much these results (Table 3). We instead repeat the above statistical procedure with a different dataset of 3 stock indices and the corresponding equally weighted portfolio: Dow Jones, MSCI World and Euro Stoxx 50 for a total of $2116 \times 3$ data points from January 2 2013 to May 28 2021. The new pair of empirical distributions (running minimum and maximum drawdown) has $2111 \times 2$ data points.

Table 3 Summary statistics of daily Returns

The stock indices’ plots in Figs. 6, 7,  8 show a similar behavior as that of the cryptocurrencies’ return series.

Fig. 6

Historical returns of Dow Jones

Fig. 7

Historical returns of MSCI World

Fig. 8

Historical returns of Euro Stoxx 50

The empirical results from a different dataset of total return indices again confirm our theoretical finds as shown in Table 4.

Table 4 Point estimators of Co-CED and CED

Conclusions

The practical relevance of path-dependent deviation measures such as the unconditional mean of the maximum drawdown attached to a traded position, or its CED at a given probability threshold is well established. Nevertheless, these measures are intrinsically relative indices of risk associated to the whole time evolution of cumulative returns over a fixed horizon such as the one-time step volatility. Potential worst case scenarios may cause abrupt change in a traded position and trigger liquidation or margin calls, even if the measurement done by the CED does not account for this. We develop a new conditional framework for deviation measures, firstly for general information set and then as a special case when the information is given by events concerning the running minimum of cumulative returns. We apply these results also for the analysis of conditional risk contributions, i.e. Euler’s allocation rules. The new framework is able to correct the underestimation experienced by CED, providing a more prudent risk measurement paradigm based on Co-CED. From the point of view of systematic risk, this can be viewed as a sort of aggregation criterion for the separate risk indices based either on the maximum drawdown or the running minimum, then translating the probabilistic link between the two into the realm of financial economics. In a sense, our refined version of conditional maximum drawdown (when conditioned on the running minimum) parallels the definition of a flash crash: a sudden and extreme price movement occurring in a short time horizon and reverting to its initial value. In the current context we can though of Co-CED as a measure of “medium” crash, since we adjust CED computed over maximum drawdown of cumulative returns (which is an estimate of the expected maximum possible cumulative drop in net asset value over the horizon), by a more informative signal of the worst case scenario representing the bottom of the market that may force investors to liquidate. So we may talk about a large downtick in the original price’s time series sometime over the horizon, not necessarily over a short time span.

The usefulness of path dependent measures as early warnings (coherently with the literature on systemic risk) is evident when these are combined with approaches aimed to catch the changing level of market rationality. The explanation of the 2008 GFC is far from being done, not even a description of facts is consistent among all authors writing about the crisis. However, the bubble story is surprising for the asymmetry, with prevailing irrationality of investors not taking profits out of the crowd. After the GFC, the extend to which politicians and regulators may trust financial economics theories and models has been questioned. First academic reaction to these critics was that financial firms used wrong input data (too optimistic, a “view of the world far more benign than it was reasonable to take” according to M. Sholes) with correct models. But data came from subjective valuation and their updates should be part of a dynamic market model. The optimal solution may become a satisfactory solution in line with the concept of bounded rationality; so far this concept has got little empirical testing for practical and theoretical reasons; an application to financial markets behavior will likely revive researcher interest, as the error margins or different valuation which may coexist are explainable through price changes, trading volumes and volatilities of both prices and volumes. Prospect Theory and Mental Accounting have provided model structures studying the interaction between stock turnover and returns, after psychologically motivated strategies. Momentum strategy is one of the strongest and most widely known selection anomalies. Unlike other anomalies, momentum did not weaken after being revealed. Prospect Theory generates a selling pressure on potential gains and a corresponding lower offer of stocks that have produced potential losses (disposal effect); this occurrence, connected with the process of Mental Accounting to update reference points, may well induce a widening gap between returns of past winners and of past losers. A common aspect of more recent studies is the tendency to look for connections between volume and a number of variables and markets. We believe that trading volume is an observable signal of the investors’ average time horizon and investors’ perceptions agreement, both governing the market. A possible approach (and a future research agenda) to cope with complex models with changing market rationality can be to explore the dynamics of path dependent indices constructed not only on prices. This may lead to useful information as early warning of bubbles and crisis and for behavioral models not easy to test with traditional methods.