Abstract
Portfolio managers regard contagion as the death of diversification. The simultaneous jump to worst decile returns for most investments in a portfolio is hard to offset by diversification alone. Our results find substantial contagion across ARP strategies, which is difficult to predict. We derive the optimal asset allocation for an ARP portfolio under contagion risk and show that the investor’s best defence is to take less portfolio leverage. In addition, he should shy away from assets that perform poorly in contagion states.




Similar content being viewed by others
Notes
Our measure is identical to Boyson et al. (2010) that look for contagion in hedge fund strategies. We are fully aware that using full sample information in the definition of worst decile returns introduces hindsight bias. However, we view this with little concern as our paper is not predictive but rather tries to understand the joint distribution of ARP strategies.
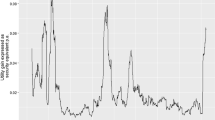
The VIX is a measure of expected stock market volatility that typically rises in times of fear when demand for option protection is rising.
Alternatively, the data could have been generated by a model with time-varying correlations and all we needed to do is to come up with good estimates for the conditional covariance matrix. Our estimates of DCC-GARCH models did not support this suspicion. Correlation changes are extremely short lived and spikey. For all practical purposes, and given rebalancing costs, no investor would follow this approach.
“Appendix 2” provides a quick derivation of this result.
References
Yacine, Aït-Sahalia, and Thomas Robert Hurd. 2016. Portfolio choice in markets with contagion. Journal of Financial Econometrics 14(1): 1–28.
Ang, A., and G. Bekaert. 2002. International asset allocation with regime shifts. Review of Financial Studies 15(4): 1137–1187.
Baltas, N., and B. Scherer. 2019. Tail risk in the cross section of alternative risk Premia. The Journal of Portfolio Management 45: 93–105.
Boyson, Nicole M., Christof W. Stahel, and René M. Stulz. 2010. Hedge fund contagion and liquidity shocks. Journal of Finance 55: 1789–1816.
Branger, N., H. Kraft, and C. Meinerding. 2014. Partial information about contagion risk, self-exciting processes and portfolio optimization. Journal of Economic Dynamics and Control 39: 18–36.
Chiang, T.C., B.N. Jeon, and H. Li. 2007. (Dynamic correlation analysis of financial contagion: Evidence from Asian markets. Journal of International Money and Finance 26(7): 1206–1228.
Das, S.R., and R. Uppal. 2004. Systemic risk and international portfolio choice. Journal of Finance 59: 2809–2834.
Diebold, F.X., and K. Yilmaz. 2009. Measuring financial asset return and volatility spillover, with application to global equity markets. The Economic Journal 119: 158–171.
Dungey, M., R. Fry, B. González-Hermosillo, and V.L. Martin. 2005. Empirical modelling of contagion: A review of methodologies. Quantitative Finance 5(1): 9–24.
Guidolin, M., and A. Timmermann. 2008. International asset allocation under regime switching, skew, and kurtosis preferences. The Review of Financial Studies 21(2): 889–935.
Hamilton, J. 1989. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57(2): 357–384.
Kole, E., K. Koedijk, and M. Verbeek. 2006. Portfolio implications of systemic crises. Journal of Banking and Finance 30(8): 2347–2369.
Kraft, H., and M. Steffensen. 2008. How to invest optimally in corporate bonds: A reduced-form approach. Journal of Economic Dynamics and Control 32(2): 348–385.
Missio, Sebastian and Watzka, Sebstian, Financial Contagion and the European Debt Crisis (2011). CESifo Working Paper Series No. 3554. Available at SSRN: https://ssrn.com/abstract=1920642 (Accessed 31 August 2011).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author thanks an anonymous referee for very helpful comments.
Appendices
Appendix 1: Data
The ARP strategy data in this paper consist of excess (vs cash) returns for 27 strategy return streams across styles and asset classes for the period 1 June 2008 to 31 January 2019. All strategies are briefly described in Table 5 and stem from a global investment bank. Our observation frequency is daily. Given the commoditization of ARP strategies, similar return profiles can be obtained from most providers and we are confident that our results generalize across all providers. Table 4 displays the risk return characteristics of our raw data. All calculations have been performed with strategy series rescaled to a 10% per annum volatility such that difference is portfolio allocations are more easily to interpret. Returns for equities, bonds and commodities are represented by the following indices: MSCI AC, Barclay/Bloomberg Multiverse and GSCI. The unconditional correlation structure between all ARP series as well as asset classes (bonds, equities and commodities) and volatility (VIX) are illustrated in Fig. 5. Panel A provides a hierarchical clustering for all series, where the similarity between strategies is expressed as distance, i.e. 1 minus correlation. The distance between strategies is typically around one as most strategies show zero correlation, which can be seen from the histogram of strategy correlations (lower triangular part of the correlation matrix) in panel (b). In general, correlations increase as strategies share the same universe or apply the same style. Examples of this are either trend following strategies (FX and Cross-Asset trend following) are close or commodity strategies (COCurve and COTS). From 465 unconditional correlations, 90% are between − 0.14 and + 027. The highest correlation is between IR carry and bonds (0.8). The second highest is between equities and commodities. Correlations with returns on equities, bonds and percentage changes in the VIX are displayed in Fig. 6. In accordance with the literature, we see that a large fraction of strategies show positive correlation with equities (i.e. loose value if equities fall) and negative correlation with volatility (i.e. loose value if volatility rises). However, in each group we also see defensive strategies with the opposite behaviour. Not surprisingly, equity strategies still show some exposures to equities, bond strategies to bonds and volatility strategies to volatility (Table 5).
Appendix 2: Theory
The investors value function at time t as a function of its state variable, \( W_{t} \), i.e. investors wealth is given by
The investor needs to find the proportion of wealth invested into \( n = 1, \ldots ,N \) risky assets subject to the dynamics of wealth given by
where w is the vector of asset weights, \( {\varvec{\upalpha}} \) and \( {\varvec{\upsigma}} \) are the vector of excess returns over cash and asset volatilities, r is cash. The vector of diffusion shocks is given by \( {\mathbf{dZ}}_{t} \), while rand jump amplitudes are denoted by \( {\mathbf{J}}_{{\mathbf{t}}} \) and occur according to a Poisson process, dQ, with intensity \( \lambda \). The Hamilton–Jacobi–Bellman equation looks like
where the last term accounts for jumps. Guessing the solution to look like
This changes the Hamilton–Jacobi–Bellman equation to:
Differentiating with respect to w, we arrive at
This equates with the equation in the main text.
Rights and permissions
About this article
Cite this article
Scherer, B. Alternative risk premia: contagion and portfolio choice. J Asset Manag 21, 178–191 (2020). https://doi.org/10.1057/s41260-020-00158-1
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1057/s41260-020-00158-1