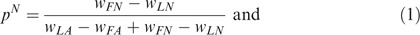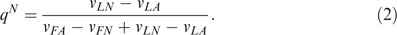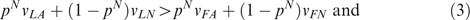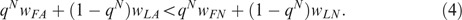The Role of Repetition and Observability in Deterring Insurance Fraud

Abstract

In this paper, I analyze an inspection game between an insurer and an infinite sequence of policyholders, who can try to misrepresent relevant information in order to obtain coverage or lower insurance premium. Because claim-auditing is costly for the insurer, ex-post moral hazard problem arises. I find that the repeated game effect serves as a commitment device, allowing the insurer to deter fraud completely (for sufficiently high discount rate) but only when the policyholders observe past auditing strategies. Under weaker observability conditions, only partial efficiency gains are generally possible. I conclude that the insurers should spend resources on signaling their anti-fraud attempts to the potential policyholders. Similar conclusions can be drawn with respect to conceptually similar problems, such as tax evasion.

Introduction

Fraudulent behavior of policyholders is a serious concern in the insurance market. Although particular estimates differ considerably, it seems likely that, for example, in the automobile insurance market, fraudulent claims account for at least 10 per cent of all indemnities paid by insurers (see Coalition Against Insurance Fraud, 2001; Boyer and Schiller, 2003 and references therein). One important reason for this is that insurance fraud is widely tolerated. According to a study by Accenture, nearly one-fourth of Americans think “it is OK to defraud their insurance companies” (Woxik, 2003). Viaene and Dedene (2004) provide a long list of justifications for insurance crimes. They are said to be perceived as victimless (or even as a legitimate means of recouping from the greedy insurance companies the money spent on overly high premiums), considered as a sport and as something that everyone does (p. 321). Another important factor is that professionals, such as physicians are willing to play along.¹ Whereas apparent weakness of the ethical considerations in the case of insurance fraud has serious negative effects for the market, it supports the seemingly strong assumption (typically made in economic models) that agents are purely self-interested.

Most theoretical work dealing with insurance fraud has focused on the instances of filing excessive or unjustified claims (see e.g. Picard, 1996; Bond and Crocker, 1997; Boyer and Schiller, 2003). However, another dangerous type of fraudulent behavior, sometimes referred to as underwriting fraud (see Viaene and Dedene, 2004, p. 315), involves concealing of risk-relevant information by the proposed insured. To name just a few examples, in auto insurance a policyholder may misreport his place of residence, identity (and especially age) of the main car user or claim history with the previous insurer.² In the United States, misrepresentation of payroll to obtain lower Workers’ Compensation premiums is another typical underwriting fraud (cf. Derrig and Zicko, 2002).

The workhorse in the literature on insurance fraud is the costly state verification model (Townsend, 1979). It is assumed that the insurer cannot, prima facie, distinguish between two or more actions that a policyholder might pursue, yet may undertake costly auditing in order to find the truth. Policyholder's action entails either admitting (or not) to be a “bad risk” (in the models of underwriting fraud) or filing (or not) a fake claim (in the models of claim fraud). The audit is typically assumed to be perfect and to come at a fixed unit cost. In the case of detecting an unlawful action, a monetary punishment (constrained by the law) may be imposed on the perpetrator. The general finding is that the insurer is best off committing to certain probability of auditing and therefore deterring fraud.³ The essential distinction can be made between the models that allow the insurer to do that (e.g. Bond and Crocker, 1997; Alary and Besfamille, 2001) and those which do not (e.g. Picard 1996; Picard, 2002; Boyer 2003; Krawczyk, 2003). Whatever the assumption, it is often made rather ad hoc, based on anecdotal evidence. Some suggestions have been made in the literature as to how a credible commitment could come about (and will be discussed here in the concluding section).

In the current paper, I endogenize the commitment possibility by nesting a single insurer–customer encounter into a supergame with a sequence of customers. Using the folk theorem for repeated games (with many short-lived agents, Fudenberg et al., 1990), I show that it is not so much the “physical” commitment, but merely observability of auditing strategy, that allows the insurer to develop reputation for “toughness” and deter any fraud (provided she is sufficiently patient).

Unfortunately, observability of mixed strategies is again a strong assumption (cf. Chatterjee et al., 2002, p. 8). I show, however, that insurer facing many customers in each period may choose to reveal her investigation choices jointly (i.e. reveal the actions, not the strategy). Then a perfect (Bayesian) Nash equilibrium arises, in which customers condition their decisions on frequency of investigations and insurer's profits approaches second best (as the discount factor approaches 1). I also consider the intermediate case where customers observe a sample from insurer's audit decisions.

The model of the stage game I am using in the paper is abstract and highly simplified, because it is meant to exhibit the central problem of commitment to randomized auditing strategy both in the case of fighting claim fraud and underwriting fraud. The main insights from my analysis of interaction with multiple agents carry over to related issues as well, such as tax compliance.

The paper is structured as follows: in Stage game section, I define a (stage) game between the insurer and a policyholder and compare the solutions under the assumption that the insurer may choose to commit to certain auditing strategy and without such a possibility (this analysis follows the lines proposed in the previous literature). In Repeated game section, the consequences of repetition of the stage game under varying assumptions regarding observability of the insurer's behavior are investigated. The concluding section points at some empirical consequences of the model.

Stage game

The general model of ex-post moral hazard in the insurance market can be presented as a three-stage game (“no-commitment game”, NCG). First, the insurer designs contracts to be offered. Next, the customers choose either a “Lawful” or “Fraudulent” action. The interpretation of the actions varies. In models of claim fraud, fraudulent action is understood as filing a fake claim. In the context of underwriting fraud, it entails a misrepresentation or withholding of relevant information, that is, declaring to be a “good risk”, while in fact being a bad one.⁴ Finally, the insurer, unaware of the policyholder's decision, chooses to investigate (audit) or not.⁵ The (minimal) assumptions regarding the structure of payoffs in the game can be described in terms of optimal responses to pure strategies of the other party in Stages 2 and 3 (i.e. after contracts have been specified).

Assumption 1

• It is in the insurer's interest to audit if and only if the policyholder plays Fraudulent; similarly, after the subgame-perfect choice of contracts has been made, it is in the policyholder's best interest to play Fraudulent if and only if the insurer does not audit.

  I shall also adopt a natural assumption that fraudulent action and auditing be welfare-decreasing

Assumption 2

• Whenever, for given auditing frequency, the policyholder is indifferent between his two actions, the insurer strictly prefers him to play lawful. Whenever, for given frequency of fraudulent actions, the insurer is indifferent between her actions, the policyholder prefers her not to audit.

  The game is presented in its normal form in Table 1.

  Table 1 Payoffs in the no-commitment game^a

  Here, first entry always denotes the payoff of the policyholder, second – of the insurer. If we denote the equilibrium choice of contract by C^N Assumption 1 thus says that v _LN (·)>v _LA (·), v _FA (·)>v _FN (·), w _LA (C^N)>w _FA (C^N), w _FN (C^N)>w _LN (C^N).

  As an obvious conclusion of Assumption 1 we note that the game has no pure strategy equilibrium yet does have a perfect equilibrium in mixed strategies.⁶ It is a simple exercise to verify that for given C, the equilibrium probabilities of playing Audit and Fraudulent, denoted by p^N and q^N respectively,⁷ are given by

  
  

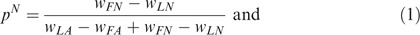
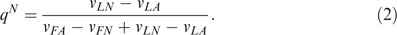
  With a slight oversimplification we can interpret the w _FN −w _LN difference as reflecting the strength of temptation (e.g. difference in premium between “good” and “bad” risks); w _LA −w _FA corresponds to the punishment following a detected fraud, v _LN −v _LA is the cost of audit and v _FA −v _FN – the cost of unaudited fraud to the insurer.

  Assumption 2 can be represented as follows:

  
  

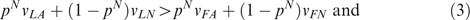
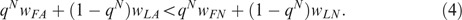
  The other game of interest, in which ex-post moral hazard is absent, is the “commitment game” (CG) with identical payoffs yet different timing of actions. Here, Stages 2 and 3 of the NCG are reversed: after setting the contracts the insurer credibly commits to the verification level. It can be easily shown that the insurer should choose the auditing frequency she would have chosen in the NCG arising after given choice of contracts (or increase it by epsilon) and the policyholders will best-respond by playing lawful with certainty. Slightly abusing the Industrial Organization terminology we could refer to the solution of the first game as Nash equilibrium and to the second game as Stackelberg equilibrium. I shall thus refer to the contract choice in the Nash equilibrium and in the Stackelberg equilibrium by C^N and C^S, respectively. Auditing frequency in the Stackelberg game will be denoted by p^S*=p^N(C^S). Further, p^N*=p^N(C^N) and q^N*=q^N(C^N) will denote the frequencies of Audit and Fraudulent, respectively, along the subgame-perfect equilibrium path of the NCG. I shall also refer to the two equilibrium payoffs of the insurer as v^N (=v _FA v _LN −v _LA v _FN /v _FA −v _FN +v _LN −v _LA ) and v^S, respectively. It is immediately obvious from earlier discussion that the latter is greater. Namely, the insurer may offer identical contracts in the CG as she did in the NCG and commit to the Nash equilibrium auditing frequency p^N (thus deterring fraud entirely). Because of the assumption on the welfare effect of the fraudulent action, the insurer is now better-off than in the Nash equilibrium. Obviously, it might be that she is able to improve her payoff even further by offering a different set of contracts.

Repeated game

The main question considered in this paper is whether or not the repetition of the NCG with a series of short-lived policyholders may bring the insurer the proceeds attainable in the CG.

To simplify the analysis, I shall assume that every policyholder interacts only once with given insurer and that insurance period is short (so there is no discounting within). The assumption that every policyholder plays the game only once may be justified by the possibility to switch to another insurer.⁸ Nota bene, multiple interaction with the same agent does not allow for full efficiency (in the adverse-selection model), because of the problem of renegotiation (see Dionne and Doherty, 1994).

The policyholder is thus a myopic (or short-lived) player, whereas the insurer, meeting one policyholder in each of an infinite sequence of periods, discounts the future using a factor of δ. This type of situation, where single long-run agent plays with a series of myopic agents, has been analyzed by Fudenberg et al. (1990). The main insight is that a version of folk theorem for these games is more limited than the standard one (Fudenberg et al., 1986). Essentially, as short-run players only care about immediate payoff, they will always best-respond in the stage game, because they cannot be punished thereafter. Further, if, given reaction correspondence of the short-run players, long-run player should make use of a mixed strategy, observability of this strategy (rather than just the actions) is essential. The long-run player's commitment to the mixed strategy is problematic, if deviations cannot be readily observed and punished by short-run players. Under non-observability only “target equilibria” survive, in which the long run player is punished or rewarded as he deviates from the “target” discounted payoff. This makes her indifferent between moves in the support of the postulated equilibrium strategy, yet means that efficiency losses obtain (recall that no punishment is ever needed on the equilibrium path in games with long-run players only, making the standard folk theorem stronger).

Strategies observable

I shall first assume that the (mixed) verification strategy is immediately and perfectly observable. The following proposition asserts that the inefficiency caused by the lack of commitment is removed.

Proposition 3

• Under full observability for sufficiently high δ, a subgame-perfect (or perfect Bayesian) Nash equilibrium exists in which in every period the insurer chooses C^Nand p^Sand policyholders play lawfully.

Proof Consider following strategies: In Period 1, the insurer offers contracts C^S and audits with probability p^S* and continues to do so until she deviates in some round and plays C^N and p^N* thereafter. Policyholders declare truthfully as long as insurer plays C^S, p^S*. If she deviates at least once, they switch to q^N. Because V^N<V^S, a sufficiently patient insurer will not deviate. Thus, threat of verification is credible and customers will declare truthfully – a perfect Bayesian Nash equilibrium.

Remark 4

• The equilibrium sketched above is just one of many that sustain the second-best. Infinite punishment phase is simplest conceptually but probably not most plausible.

All actions observable

As Fudenberg et al. (1990) in their Proposition 4 assert, when short-run players cannot observe mixed strategies on part of the long-run player, the latter can at equilibrium secure at most the payoff associated with this action in the support of her strategy which yields her the least. In our case, when policyholders play lawfully, it is the action Audit, so, effectively, she can just as well audit all claims. The intuitive reason for this inefficiency is that, if short-run players have to condition their actions on the history, the insurer will in general not be indifferent between the two actions she may take, so she will not be willing to randomize, unless she is punished for overly low frequency of audit, which must happen along the equilibrium path.

Proposition 5

• If the insurer–policyholder (stage) game is played in periods 1,  2, … , there is no perfect Bayesian equilibrium in the supergame giving the insurer profits higher than repeated play of the single-round equilibrium, which is V^N/1−δ.

Proof Follows immediately from Proposition 4 in Fudenberg et al. (1990).

The logic behind this result is quite straightforward. Suppose the insurer can secure overall discounted profit in the supergame V^SG higher than V^N/1−δ. Because, due to stationarity,⁹ we have that V^SG⩽V₁+δV^SG where V₁ denotes the expected profit in the first round, it must be that V₁>V^N. Given Assumption 2, that can only happen if in the first round (for some chosen contract C¹) either the frequency of fraudulent action or the auditing frequency is below the Nash level. Suppose the first is the case. Given that policyholders will best-respond, it requires that auditing frequency be at least at the Nash level, so the insurer must find the auction Audit at least as good as No Audit. Therefore, the former must also yield, in the first round, more than V^N, which is a contradiction because profitability of the auction Audit is at most V^N when policyholders play they Nash equilibrium mixed strategy and strictly less when they choose Fraudulent less often, as supposed. The only possibility is therefore that the frequency of auditing be lower than in the Nash equilibrium, which would however imply that all policyholders choose the fraudulent action. Then the expected payoff associated with the action No Audit is obviously lower than V^N so it cannot be played in the equilibrium yielding more than V^N in the first round, again contradicting the supposition.

It may be argued that the difficulty of committing to a mixed strategy is driven by the assumption in the literature started by Fudenberg et al. (1990) that the long-run player only interacts with one short-run player at a time. This appears highly artificial in the context of insurance markets, where in fact, companies may deal with thousands of customers every day. Thus, even if the actual randomization is unobservable, the equilibrium sustaining Stackelberg solution may be based on frequency of verifications in a single period. Because all transactions take place at (approximately) same time, insurer is indifferent between verifying particular declarations, thus may credibly commit to randomization.

Formally, suppose that in each period t the long-run player designs contract C^S, meets n short-run players and performs [p^Sn]+1 audits.¹⁰ It is therefore optimal for the customers to report truthfully. Whenever the insurer deviates from her policy, all players switch to Nash response. It is clear that with sufficiently high n, average insurer's profit approaches V^S.

Proposition 6

• As number of short-run players active per period increases, and δ approaches 1, maximum per-round profit approaches V^S.

  Proof Analogous to the proof of Proposition 3.

  It is interesting to consider the issue that arises in a slightly richer model, namely the question regarding optimal revelation period. Assuming, which seems plausible, that the insurer has some discretion over frequency and precision of reports regarding her verification policy, what is the optimal way of disclosing this information? In the current model, if n is large (so that the losses from overshooting the required frequency of verification are negligible), such reports should basically be made as often as possible, thus decreasing per-period discount rate. Although this may look as a highly stylized solution, recent tendency in the industry to establish Special Investigation Units within insurance firms may be considered precisely as a signal that efforts to deter fraud are continued at constant level.

  In a richer model however, allowing for observable heterogeneity of customers (some making the insurer suspicious, some not, see e.g. Schiller, 2003), pooling more observations into one report may help the insurer allocate the investigation efforts more effectively, especially if there is some time variation in the frequency of unlawful actions (e.g. triggered by legal changes, spectacular insurance scams being publicly known etc.). I do not know any detailed analysis of this issue and suspect it can be severely hindered by lack of relevant empirical data.

  If one wishes to weaken the assumption further, for example supposing that observed actions are forgotten after some number of periods, the Stackelberg solution efficiency also obtains, yet for higher δ values (possibly for no values of δ smaller or equal to 1).

Some actions observable

In this subsection, I allow for even less information, namely I investigate the situation in which customers have no access to insurer's reports regarding auditing frequency or cannot take them at face value. Instead, they base their decisions on a (small) sample of cases readily available to them – spectacular scams described in the media, cases of (un)successful fraud attempts¹¹etc. It turns out that the insurer cannot obtain the Stackelberg efficiency.

Intuitively, the explanation is simple. In the Stackelberg equilibrium, all customers must declare truthfully. In equilibrium, short-run players best-respond to stage game actions of the insurer. Therefore, they will declare truthfully iff frequency of investigation dictated by the supergame equilibrium strategy is sufficient.¹² They will do so no matter what they observe. Therefore, insurer has an incentive to deviate and audit less.

To simplify the analysis I impose a natural stationarity condition by assuming that along the equilibrium path, players use same stage-game strategies. I cannot assert that no perfect equilibrium violating this intuitive condition achieves greater efficiency.

I assume that consumer i in period t observes a random sample of interactions from the previous period of size n _it and in each case learns whether the insurer decided to investigate or not. In general, n _it may be stochastic, varying over time and across consumers. However, for the ease of exposition, I shall assume it to be constant denoted by m. I also assume that m is “small” compared to n, the number of customers in the previous round, such that auditing more than 1−m/n results in all policyholders reporting truthfully and profits being lower than V^N. Strategy s _it of a policyholder is thus described by a vector of m+1 zeros and ones, signifying decisions whether or not to cheat conditional on observing 0,1, …, m verifications in the sample. Insurer's auditing strategy is described by a single parameter p. Suppose p is greater than the Nash equilibrium value p^N(C^m) and not greater than 1−m/n. Clearly, the sole optimal response on part of the consumers is to always declare truthfully: s _it =(0, 0, …, 0). Given this response pattern, insurer may profitably deviate from p (e.g. to zero verification frequency) and the customers will not realize that. Similar argument shows that in equilibrium p cannot be strictly smaller than p^N(C^m). If p=p^N(C^m), both possible actions of the consumers are optimal. Now, consider overall frequency of fraudulent actions q, determined by s _t =(s_1t, s_2t, …, s _Nt ) and auditing frequency (in the previous period) p. If q is “low”, the insurer is tempted to lower p, if q is “high”, he wishes to increase it. The threshold – equilibrium value q^m – depends on the immediate benefit from switching from auditing to non-auditing or vice versa and on the discounted cost/benefit from altering the signals obtained by the consumers in the next period. The most profitable (end efficient) equilibrium is the one in which threshold level of q is possibly lowest. Therefore consumers’ (mixed) strategy vector should make non-auditing more costly, that is it is the (very intuitive) case in which consumers observing low number of verifications tend to cheat, whereas those observing high number of investigations behave lawfully.

This gives an equilibrium. Insurer offers contract C^m and audits with probability p^m. Each consumer observes v _it audits in the sample of n policies, checks the value of the cumulative distributions function F(v _it ) (which is known, since p^m is known) and decides to cheat iff it is smaller than or equal than certain threshold q^m.¹³ The latter is such that, given this consumers’ strategy, insurer is indifferent between auditing and not auditing any single claim.

The critical difference between this setup and the case of a single no-commitment stage game (or a sequence of such games with no between-period information whatsoever) is in the deterrence value of playing the action Audit. Let us investigate this deterrence benefit, DB. It is proportional to the expected number of individuals who will be just below the threshold q^m:

where p^f represents auditing frequency in the future. Along the equilibrium path, p^f will be equal to p^m. The value of Pr(·) in the expression above may be approximated, using normal distribution, as

¹⁴ The expression therefore simplifies to:

Because decreases in absolute value as m increases and φ(·) has a single peak at 0, DB will generally increase if q stays constant. The new payoff matrix is presented in Table 2.

Table 2 Payoffs in the NCG with limited observability

Whether this game has an equilibrium in pure strategies depends on the value of DB. If it is sufficiently high, strategy “Audit” dominates and the equilibrium is (L, A). Otherwise, an equilibrium in mixed strategies arises as before. Of course, equilibrium frequency of auditing, given C^m, is not different than it was in a single NCG, equal to p^N(C^m), but policyholders will now play fraudulent with the frequency q^m solving the equation:

This frequency is lower than in the Nash solution of the original NCG, decreasing, as shown before, in m but strictly positive.

Thus we have established.

Proposition 7

• When customers base their decisions on sampling information from the last period, the payoff the insurer can achieve is strictly lower than v^S but strictly higher than v^Nand non-decreasing in m.

In other words, partial observability of verification frequency increases efficiency but does not allow obtaining the second-best.

Conclusion

Lack of possibility to commit to sufficiently high level of costly state verification (be it content of the policy or validity of the claim) is a substantial issue in the theoretical literature on deterring insurance fraud. Recent contributions suggest some ways in which this problem can be overcome. Most notably, Picard (1996) and Melumad and Mookherjee (1989) propose outsourcing the investigation to a third party. This attractive idea has its problems, however, including transaction costs, moral hazard and possibility of renegotiation.

Interestingly, more data-oriented papers (e.g. Artis et al., 1999; Cohen, 2005; Chiappori et al., 2006) and case studies rarely mention the problem of committment. This paper provides some intuition how firms can effectively deter fraud while keeping the investigation unit within their own structures. More specifically, I show how putting a single insurer–policyholder interaction into the natural dynamic context of the supergame with many clients reduces the commitment problem. In the natural subgame-perfect equilibrium, fraudulent behavior becomes less frequent because insurer can credibly commit to maintaining the sufficient auditing level. Indeed, if she ever deviates, she will suffer more frauds in the future. The only concern of the insurer is therefore to convey credible information regarding frequency of auditing. Admittedly, this can pose a challenge to the public relations policy, as the firm may otherwise try to maintain an image of mutual trust and friendliness in relations with its customers. This actually explains the emergence of independent organizations, like the Coalition Against Insurance Fraud, established to achieve a “long-term commitment” to “bring the crime wave to its knees” (CAIF website). In a sense, the insurers seem to be only outsourcing the dissemination of information regarding auditing efforts, not the auditing process itself. I show also that even partial disclosure of relevant information regarding auditing frequency via informal channels (observation of a small sample of cases, e.g. in the family or neighborhood) can reduce the frequency and thus cost of fraud.