Introduction

Modern electronics makes use of the electronic charge to transport information. Because of electron scattering in metals and semiconductors, electronic devices experience resistance which results in significant energy loss. Due to Joule heating and dissipation miniaturization of transistors and integrated circuits is about to reach its technological limit. One way of overcoming these limitations is the use of the electron spin to store and process information. Research in the fast-developing field of spintronics mainly focuses on the development of technologies based on spin-polarized currents like spin valves that in the past have revolutionized the capacity of hard disk drives1,2. These efforts led to the emergence of the field of “magnonics” that promises low energy consumption. This technology uses spin waves (“magnons”) to process and store information and exploits the advantage that magnon-based devices can be easily tuned by an external magnetic field3,4. Among candidate materials for magnonic applications, magnetic van der Waals crystals are of special interest since a single layer can be exfoliated that allows us to build complex heterostructures5,6. One example is MnPS3 that is considered for magnon transport7 and detection of antiferromagnetic states8. A key issue in developing magnonic materials is to control the direction of propagation of the spin waves at the surface of artificial nanostructures. The discovery of magnetic crystals where spin waves are robust at the surface and can propagate only along a single direction, because they are topologically protected, has prompted new ideas for future magnonic applications9. Non-trivial topological states can result from spin-orbit interactions that open a gap in the magnon Dirac cone10,11. The spin-orbit coupling is at the origin of the antisymmetric Dzyaloshinskii-Moriya (DM) interaction in magnetic crystals12 that induces the magnon-Hall effect observed in ferromagnetic insulators13,14. Recently, it was proposed that dipolar interactions have a similar effect as the DM interaction15,16 that paves the way for the realization of topological artificial nanostructures17,18.

Dipolar interactions are always present in magnetic solids. They are direction dependent and long-range in contrast to exchange interactions. This property induces frustration in the lattice as in general it is not possible to satisfy all interactions simultaneously. The problem of determining whether a lattice of ordered magnetic dipoles can exist was addressed by Luttinger and Tisza19. They demonstrated that the face-centered and body-centered cubic lattices display ferromagnetism at low temperature while for the simple cubic lattice the classical ground state is a collinear antiferromagnet. The Mermin–Wagner theorem20 does not apply in the case of long-range potentials and the absence of order in two-dimensional (2D) magnets with dipolar interactions does not generally apply. For a triangular lattice with solely dipolar interactions21, indeed long-range order is predicted. For both the square and honeycomb dipolar lattices, the classical ground state exhibits a continuous degeneracy22,23. Finally, in the geometrically frustrated Kagome lattice, no ground state satisfies the condition that the spin length is constant on all lattice points and long-range ferrimagnetic order is predicted with numerical simulations24.

In this work, we report an analysis of the magnetic ground state and excitations in the van der Waals magnet ErBr3 which was shown to undergo a magnetic phase transition to a continuously degenerate non-collinear 2D order below T = 280 mK25. We show that the magnetic ground state in this crystal is explained by dipolar interactions between the Er3+ moments. Calculation of the dispersion of the magnetic excitations using the mean-field random-phase approximation (MF-RPA), which includes dipolar interactions and crystalline electric-field (CEF) anisotropy, describes the inelastic neutron-scattering (INS) data. Using our simulations of the magnetic excitations for the dipolar honeycomb lattice, we show the presence of a Dirac cone at the K-points of the Brillouin zone when the configuration of dipoles possesses inversion (I) and time-reversal (T) symmetry. A gap opens at the Dirac points between the acoustic and lowest optical branch as the degeneracy angle between spins in the two sublattices of the honeycomb structure is varied and the IT symmetry of the magnetic structure is lifted.

Results

Crystal and magnetic structure of ErBr3

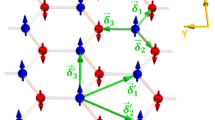
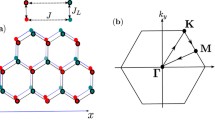
ErBr3 crystallizes in the BiI3 structure26 with the rhombohedral space group R-3 (no. 148) and lattice parameters a = b = 7.005 Å and c = 18.89 Å at T = 1.5 K25, as shown in Fig. 1a. In this layer-type structure the Br− ions adopt a hexagonal densest packing (AB) and Er3+ ions occupy in an ordered way 2/3 of the octahedral voids between every other layer (2/3c). The layer stacking along the c-axis results in a sequence A2/3cBA2/3cBA2/3cB with three Er3+ honeycomb layers per unit cell. The Er3+ ions are located on site (6c) at (0, 0, ±z), (0, 0, ±z) + (2/3, 1/3, 1/3), and (0, 0, ±z) + (1/3, 2/3, 2/3). In this crystal z = 1/6 and the rare-earth ions form a perfect honeycomb lattice. The magnetic structure of ErBr3 was determined by powder neutron diffraction25. Magnetic order sets in below T = 280 mK and down to T = 50 mK only 2D order is observed. The magnetic ordering vector k0 = (1/3,1/3,0) triples the volume of the magnetic unit cell to \(\sqrt{3}a\,\times \sqrt{3}a\,\times\, c\) with axes rotated by 30° from the crystallographic cell, see Fig. 1b. The ordered magnetic moments are located in the honeycomb plane and amount to μ = 4.7 μB at T = 50 mK. The honeycomb lattice is composed of two trigonal sublattices. The Er3+ ions on each sublattice exhibit a 120° antiferromagnetic order with opposite chirality, see Fig. 1b. The magnetic ground state has an infinite degeneracy with respect to in-plane rotation of the ordered moments by an arbitrary angle Ψ with opposite signs for the two sublattices25, see Fig. 1c.

Fig. 1: Crystal and magnetic structure of ErBr3.
figure 1

a Crystal structure of ErBr3. Br− ions octahedrally coordinate Er3+ ions that form honeycomb layers stacked along the c-axis. b Honeycomb layer of Er3+ ions at z = 1/6 with ordered magnetic moments of 4.7 μB (black arrows) for a spin configuration given by angle Ψ = 0. The two trigonal sublattices of the honeycomb are shown as blue and red spheres. The crystallographic and magnetic unit cells are shown as black and green lines, respectively. c The classical magnetic ground state is continuously degenerate and the magnetic moments can be rotated in opposite direction by varying the angle Ψ. In panel c, Ψ = π/6.

Full size image

In the mean-field approximation, the magnetic ground state is determined by the eigenvector of the largest eigenvalue of the Fourier transform of the exchange interaction tensor27. The Hamiltonian with purely dipolar interactions is written

$$H=-\frac{{(g{\mu }_{B})}^{2}{\mu }_{0}}{8\pi }\mathop{\sum}\limits_{i,j}{{{{{{{{\bf{J}}}}}}}}}_{i}\cdot \overline{\overline{D}}(ij)\cdot {{{{{{{{\bf{J}}}}}}}}}_{j}$$
(1)

and

$${D}_{\alpha ,\beta }(ij)=\frac{3{({{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{j})}_{\alpha }{({{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{j})}_{\beta }}{| {{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{j}{| }^{5}}-\frac{{\delta }_{\alpha ,\beta }}{| {{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{j}{| }^{3}}.$$
(2)

α, β = a, b, c are the crystal directions in Cartesian coordinates and Ri is the position vector of the i magnetic ion. The dispersion of the eigenvalues of the Fourier transform of the dipolar tensor along κ = (q, q, 0) for the ErBr3 crystal with six Er-ions in the chemical cell is shown in Supplementary Fig. 1 of Supplementary Note 1. The largest eigenvalue has a maximum at k0 = (1/3, 1/3, 0) in agreement with the propagation vector of the magnetic structure measured in ErBr3. This particular non-collinear magnetic ordering cannot be reproduced by frustrated Heisenberg interactions28. The temperature of the magnetic phase transition calculated with mean-field theory29 \({T}_{{{{{{{{\rm{MF}}}}}}}}}=\max \{{\lambda }_{{{{{{{{{\bf{k}}}}}}}}}_{0}}/{{{{{{{{\rm{k}}}}}}}}}_{B}\}/3 \sim 0.3\,{{{{{{{\rm{K}}}}}}}}\) is close to the ordering temperature of the Er moments measured by neutron diffraction. Mean-field theory predicts the same magnetic ground state that is observed in ErBr3 and agrees with the spin order obtained by Rozenbaum23 for magnetic dipoles on the bipartite honeycomb lattice. The magnetic ground state is continuously degenerate and the equivalent spin structures are defined in terms of an arbitrary angle Ψ, as shown in Fig. 1c. Supplementary Fig. 2 shows the dependence of the ground state energy upon the lattice parameter c of the crystal structure of ErBr3. The dipolar energy is constant for a lattice parameter c > 10 Å that indicates that interlayer interactions become negligibly small above that value. With a lattice parameter c = 18.89 Å and an interlayer distance of c/3 = 6.3 Å the 2D limit is reached in ErBr3.

Spin waves

To calculate the dispersion of the magnetic excitations we used the MF-RPA method that treats the single-ion interactions (crystal-field and mean-field Hamiltonians) exactly while the interactions between the magnetic ions are considered in the random-phase approximation30. The INS measurements of the crystal-field splitting of ErBr3 are presented in Supplementary Note 2 and the analysis of the data explains the temperature dependence of the single-ion susceptibility shown in Supplementary Fig. 5. In ErBr3, the first crystal-field level is located at 1.5 meV (see Supplementary Fig. 5), much higher than the energy scale of the dipolar interactions; the spin system can be approximated by a S = 1/2 doublet with effective anisotropic g-factors as detailed in Supplementary Note 3. For ErBr3, we obtained a large easy-plane anisotropy with gx = gy = 9.4 and gz = 0.1.

In MF-RPA the spin-wave excitations appear as poles in the dynamical susceptibility tensor \(\overline{\overline{\chi }}({{{{{{{\bf{q}}}}}}}},E)\),

$$\overline{\overline{\chi }}({{{{{{{\bf{q}}}}}}}},E)={\left[\overline{\overline{1}}-{\overline{\overline{\chi }}}_{0}(E)\overline{\overline{D}}({{{{{{{\bf{q}}}}}}}})\right]}^{-1}{\overline{\overline{\chi }}}_{0}(E),$$
(3)

where \({\overline{\overline{\chi }}}_{0}(E)\) is the single-ion susceptibility and \(\overline{\overline{D}}({{{{{{{\bf{q}}}}}}}})\) the Fourier transform of the dipolar interactions. Because the magnetic moments of ErBr3 in the 2D phase form a non-collinear structure, it is convenient to introduce local coordinates for each spin in the magnetic cell with the quantization axis pointing along the spin direction, so that after transformation the single-ion susceptibility is the same for every magnetic site in the unit cell30. The inelastic neutron cross-section S(κ, E) is then proportional to the imaginary part of the dynamical susceptibility

$$S({{{{{{{\boldsymbol{\kappa }}}}}}}},E)=\frac{1}{\pi }\frac{1}{1-\exp (-E/{k}_{B}T)}\frac{1}{N}\mathop{\sum}\limits_{\alpha ,\beta }\mathop{\sum}\limits_{u,v}\left({\delta }_{\alpha ,\beta }-\frac{{\kappa }_{\alpha }{\kappa }_{\beta }}{| {{{{{{{\boldsymbol{\kappa }}}}}}}}{| }^{2}}\right)\Im {\chi }_{u,v}^{\alpha ,\beta }({{{{{{{\boldsymbol{\kappa }}}}}}}},E)$$
(4)

with κ = τ + q the scattering vector and τ a reciprocal lattice vector; u, v number the N Er-ions in the magnetic cell and α, β = a, b, c. Equation (4) is given in the crystal frame and hence, the \(\Im {\overline{\overline{\chi }}}_{u,v}({{\boldsymbol{\kappa}}} ,E)\) matrices are evaluated in the rotated local coordinate system.

For the spin-wave calculations, only interactions within a single honeycomb layer were considered as the dipolar interactions between the planes are negligibly small. The spin-wave dispersion is shown in Supplementary Fig. 7. For scattering vectors along (0, q, 0) an acoustic mode and three optic branches are well observable, while the other two spin-wave branches have a considerably lower intensity. Along this direction in reciprocal space S(κ, E) does not change appreciably when Ψ is varied for the optical branches above E ≃ 0.1 meV and no crossing of the acoustic mode with an optical branch occurs.

The INS measurements in ErBr3 were performed with an energy resolution of about 70 μeV and the spin waves that have an energy E < 0.1 meV are hidden by the incoherent scattering at the elastic position. Fig. 2a shows representative INS measurements along (0, q, 0) at T = 80 mK together with the result of MF-RPA. Additional INS measurements are shown in Supplementary Fig. 6 together with a plot of the magnetic Brillouin zone where the scan directions are indicated. Only an overall scale factor is used to adjust the INS intensity with the MF-RPA calculations. The peaks in the INS spectrum at ~0.2 meV correspond to the dispersion of the highest visible magnon branch. Both the dispersion of the spin waves and the intensity of the INS are well reproduced. In Fig. 2b, we compare the dispersion of the spin waves in ErBr3 with the MF-RPA calculations. It can be observed that the calculated spectrum of S(κ, E) is in agreement with the INS data.

Fig. 2: Spin-wave measurements in ErBr3.
figure 2

a Representative inelastic neutron scattering measurements of the spin-wave excitations in ErBr3 compared with the result of mean-field random-phase approximation (blue lines). The red line is a fit of the incoherent scattering measured at momentum transfer κ = (2/3, –4/3, 0) and at T = 6 K, which is well above the temperature of the phase transition T = 280 mK and in the paramagnetic phase where there are no propagating coherent spin waves. The sum of both contributions is shown by the black line. Error bars are standard deviations given by the square root of the neutron counts. b False color plot of the inelastic neutron cross-section S(κ, E) along κ = (0, q, 0). In the calculations, we used a linewidth Γ = 0.07 meV in the single-ion susceptibility to approximate the energy resolution of the spectrometer (see Supplementary Note 3). The points represent the spin-wave dispersion in ErBr3 obtained from a fit with a single Gaussian. Magnetic excitations below the energy E = 0.1 meV were not accessible in the experiment. The error bars are a result of the Gaussian fit.

Full size image

Discussion

The electronic band structure of materials with a honeycomb structure, like graphene, exhibits Dirac points at the corners of the Brillouin zone (the K-points in Supplementary Fig. 6c) where the electronic bands cross. Close to the K-point the electronic bands have a linear dispersion that corresponds to the dispersion of a relativistic and massless particle31. It was shown that the spin waves of a Heisenberg ferromagnet with a honeycomb structure have Dirac cones32,33 around the K-point opening the possibility of producing magnetic Dirac materials. In agreement with these predictions topological magnons have been observed as Dirac massless bosons in the ferromagnet CrBr334. The acoustic and optical spin-wave branches cross at the K-point of the Brillouin zone boundary and have a linear dispersion analogous to the electronic band structure of graphene. Magnon Dirac cones are not only found in ferromagnetic insulators and topological magnons protected by symmetry have been observed in the 3D antiferromagnets Cu3TeO635,36,37 and CoTiO338. In contrast, a magnon band gap is observed at the zone boundary in CrI3. The origin of the gap is still debated and has been associated either with the DM interaction between next-nearest neighbors on the honeycomb lattice39 or magnon-phonon coupling40. In magnetic insulators, the DM interaction plays the role of the spin-orbit interaction present in graphene and leads to avoided band crossing of magnons. According to the bulk-edge correspondence41, magnons, in the gapped phase, can propagate uni-directionally along the surface or edges which opens the possibility of producing magnetic counterparts of topological insulators.

Figure 3a shows the dispersion of the spin waves for ErBr3 along the (q, q, 0) direction. As the magnetic ground state is degenerate, we have performed the calculations for different values of Ψ for the magnetic moments of the Er-sublattices. The dispersion of the spin waves for the dipolar honeycomb lattice shows a Dirac cone at the K-point when the spins in ErBr3 form a periodic vortex structure with Ψ = 0 (Fig. 3a). When Ψ is varied an anti-crossing of the lowest optical branch with the acoustic branch appears at the K-point of the magnetic Brillouin zone. The size of the energy gap between the two branches depends on Ψ as shown in Fig. 3b and reaches a maximum for Ψ = π/6. The splitting between the acoustic and optic branch decreases again for values of Ψ larger than π/6; finally, the two branches form a Dirac cone again when the arrangement of the Er moments corresponds to a periodic vortex structure with Ψ = π/3 (Fig. 3a). Furthermore, the variation of Ψ from 0 to 2π produces six distinct spin structures on the honeycomb net corresponding to three vortex positions with opposite chiralities where the Dirac cones are present in the spin-wave spectrum at the K and K’ points.

Fig. 3: Magnon gap in the dipolar honeycomb lattice.
figure 3

a Simulation of the inelastic neutron cross-section S(κ, E) along the momentum transfer κ = (q, q, 0) for selected Ψ. Note the opening of a gap at κ = (2/3, 2/3, 0) between the acoustic and the lowest optical mode at the energy E ≈ 0.083 meV when the spin configuration given by angle Ψ is varied. The color bar represents the calculated intensity of the inelastic neutron cross-section. b Dependence of the magnon band gap as a function Ψ at κ = (2/3, 2/3, 0). c Calculation of the spin-wave dispersion close to the Dirac point for Ψ = −5.6 × 10−4 π, 0, and +5.6 × 10−4 π, respectively.

Full size image

For Ψ = n × π/3 (n an integer), the acoustic and the lowest optical spin-wave branch cross at the K-point with a linear slope, and a Dirac cone is found at an energy of E ≈ 0.083 meV, as shown in Fig. 3c. We calculated a Berry phase γ = ±π (see Fig. 4a and Supplementary Note 4) that reflects the degeneracy of the two magnon branches at the Dirac points and shows that the topology of the magnon dispersion in ErBr3 mimics the topology of the electronic band structure in graphene. Our results demonstrate that Dirac cones are not only present in honeycomb magnets with Heisenberg interactions, but also in van der Waals crystals like ErBr3, where long-range dipolar forces are the primary magnetic interaction.

Fig. 4: Berry phase and Berry curvature in the dipolar honeycomb lattice.
figure 4

a The Berry phase associated with the Dirac cone (Ψ = 0°) is either +π (represented in yellow) or –π (blue). The Berry curvature Ω(k) in ErBr3 calculated for the acoustic magnon branch: b Ψ = −5°, c Ψ = 5°, Ψ = 30° and Ψ = 55°. Ψ is the angle representing the spin configuration. The Brillouin zone boundary is outlined with dashed lines. The color bar shows the magnitude of the Berry curvature.

Full size image

As in Cu3TeO6, Dirac points are present in the spectrum of magnetic excitations due to the invariance of the magnetic structure under combined inversion and time-reversal symmetry operations35,36,37. When Ψ ≠ n × π/3 (n an integer), the symmetry of the spin structure is broken which generates a finite Berry curvature as shown in Fig. 4b. In Fig. 4c and Supplementary Fig. 8, we show the evolution of the Berry curvature calculated for the magnon acoustic branch which is well separated from the other branches. The Berry curvatures at the K and K’ points have the same magnitude but opposite signs as is the case in graphene42. For degeneracy angles close to Ψ = 0, the Berry curvature Ω(k) is peaked around the K and K’ points and diverges when Ψ → 0. With increasing values of Ψ we observe that Ω(k) continuously broadens and weakens but remains centered around the K and K’ points. The Berry curvature finally disappears at Ψ = π/6 when the gap between the acoustic and optical branch has its maximum value. Upon increasing the angle Ψ further, the Berry curvature reappears close to the K and K’ points albeit with opposite signs. The Berry curvature of the dipolar honeycomb magnet hence depends on the size of the spin gap and can be manipulated by varying the angle Ψ. The Chern number C is equal to 0 when the Berry curvature is integrated over the entire Brillouin zone. Although C = 0 indicates a topologically trivial magnon insulator phase, when the integration of Ω(k) is restricted around a single Dirac point we numerically obtain for Ψ = 1. 5° CV ≈ ±1/2 at the K and K’ points that is a prerequisite for the quantum valley Hall effect43,44. A non-trivial Berry curvature is also at the origin of the magnon valley transports that were recently reported in refs. 45,46. For the dipolar honeycomb lattice, a topological phase transition occurs at Ψ = 0 where the spin gap closes at the Dirac points and CV changes sign. As the Berry curvature is antisymmetric with respect to the transition point, a topological magnon can propagate along the interface of two spin-domains located on opposite sides of the phase boundary47. It is worth restating that these considerations hold for purely dipolar interactions. If exchange interactions are present, long-range ordering will occur with the moments normal to the plane48.

In conclusion, we have shown that ErBr3 serves as a model crystal for the dipolar antiferromagnet on the honeycomb lattice. The classical magnetic ground state forms a degenerate non-collinear vortex structure and we have found that the lowest magnon bands evolve from Dirac magnon excitations to a topological phase with non-trivial Berry curvature by varying the phase Ψ that defines the spin configuration. The application of an external magnetic field lifts the degeneracy of the ground state and can be used to select a particular spin configuration by varying the direction of the magnetic field22. As van der Waals magnets can be cleaved this could be relevant for future investigations of magnon currents in honeycomb lattices. Our results suggest that if artificial dipolar honeycomb lattices can be built, it would have the potential to be extremely useful for magnonic devices since the energy at which the magnon band crossing occurs can be adapted by varying the size of the magnetic moment or the lattice spacing that allows us to engineer the magnon band structure49,50.

Methods

Single crystal of ErBr3 and characterization

The single crystal of ErBr3 was synthesized according to the method described previously in ref. 25. The magnetic susceptibility was measured with an MPMS-5XL SQUID system (Quantum Design).

Neutron experimental setup

The CEF splitting was determined with the thermal-neutron spectrometer Eiger at the SINQ spallation source. The spectrometer was operated in the constant final energy mode with kf = 2.662 Å−1. To maximize the intensity the monochromator was double focused and the analyzer was horizontally focused. With this configuration the energy resolution is about ΔE = 0.8 meV at the elastic position. Contamination by higher-order neutron wavelengths was eliminated by a PG002-filter installed in the scattered beam. The dispersion of the magnetic excitations was measured with the cold-neutron three-axis spectrometer IN14 at the Institut Laue-Langevin. The spectrometer was operated in a similar configuration as for the previous measurements albeit with kf = 1.15 Å−1 that resulted in an improved energy resolution of 70 μeV. A cold Be-filter, which scatters off neutrons with wavevectors longer than kf = 1.55 Å−1, was used to reduce the background and avoid spurious scattering. For these measurements, a single crystal of approximately 0.5 cm3 was mounted inside a dilution refrigerator and cooled down to the base temperature of T = 80 mK that is well below the ordering temperature of the Er3+ moments at T = 280 mK.