Abstract
Anthropogenic warming can alter large-scale circulation patterns in the atmosphere, which could have serious consequences for regional climate impacts and extreme weather. Observed thermodynamic changes in boreal extratropics have been attributed to human emissions with high confidence, but most circulation changes have not. In particular, not only that in the previous suite of climate models most models do not capture the recent boreal summer storm tracks weakening, but also a quantification of the role of human emissions in the recent storm tracks weakening has not been conducted to date. Here we use the latest suite of climate models, which are found to adequately capture the recent storm tracks weakening, and show that this weakening is attributable to anthropogenic emissions. Human emissions have resulted in more-rapid warming of the high latitudes, and the associated reduction in poleward temperature gradient has weakened the storms. The physical consistency between models and reanalyses increases our confidence in the projected weakening, which presents regional risks including hot-dry extremes in summer.
Similar content being viewed by others
Introduction
Near-surface warming over the last decades have been attributed to anthropogenic emissions with high confidence1. Several other thermodynamic aspects of global warming have also been attributed to human activity, including ocean and atmosphere warming patterns2,3, increase in tropopause height4, Arctic sea-ice melting5 and the enhanced warming of the Arctic relative to lower latitudes (or ‘Arctic Amplification’)6. Moreover, thermodynamic drivers behind the increase of extreme weather, like heatwaves or heavy rainfall, have been attributed with high confidence1. Confidently attributing a detected trend to anthropogenic emissions requires a proper understanding of the underlying physics as well as an adequate representation of those physics in climate models.
Climate models also project changes in the large-scale atmospheric circulation1,7,8,9,10 (e.g., changes in jet stream, storm tracks, Hadley circulation, etc.). Some of these circulation changes have already been observed and attributed to anthropogenic emissions, including, the weakening of boreal summer jet stream11,12 and the expansion and weakening of the Hadley circulation13,14. In contrast, the role of human emissions in recent storm tracks changes is largely unknown1.
Changes in storm tracks can have pronounced implications for the regional climate, as they define weather variability in the extratropics including extremes (e.g., weather systems, heat waves, cold spells, etc.). Storm tracks not only affect our day-to-day weather, but also the climate itself as they account, over multi-decadal timescales, for most of the poleward energy transport (e.g., heat and moisture) across the mid-latitudes. It is thus critical to assess the impacts of human emissions on mid-latitude storm tracks to better constrain extratropical climate model projections and increase our preparedness for future climate change. However, unlike thermodynamic changes, attributing any historic storm track changes to human activity is much more challenging. Low-frequency chaotic variability (i.e., the atmosphere can exhibits trends on decadal timescales simply due to internal variability) as well as biases in climate models generate large uncertainty in estimating any human-induced circulation changes15,16,17.
Specifically, using observation-based datasets (i.e., reanalyses), previous studies reported that the boreal mid-latitude summer storm tracks have weakened since 197918,19,20,21. This weakening is evident in both storm tracks intensity (so called Eddy Kinetic Energy, EKE)18,20,21,22 and in the number of cyclones19. Climate models from the Coupled Model Intercomparison Project 5 (CMIP5) show a clear weakening of summer storms in response to anthropogenic emissions, however, the magnitude in most models is small compared to reanalyses trends18,19,22. The CMIP5 multi-model mean (MMM) response reaches the level of the current weakening in reanalyses only by the end of the century under a very high emission scenario18. This suggests that most CMIP5 models either underestimate internal low-frequency variability or the forced response to natural or anthropogenic emissions, or a combination of both. In addition, the role of human emissions in the recent storm tracks weakening has not been quantified to date. The latest report from the Intergovernmental Panel on Climate Change (IPCC) therefore concluded that there is generally ‘low confidence’ in human-induced historic changes in boreal extratropical storm tracks1.
Results
Recent storm tracks weakening
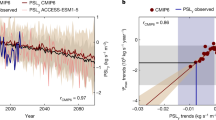
Here we revisit this models-reanalyses discrepancy using the latest suite of global climate model (CMIP6), forced with historical emissions through 2014 and the SSP5-8.5 scenario thereafter, and the latest reanalyses products (Methods). Over the 1979–2020 period, summertime (June-August, JJA) NH mid-latitude tropospheric EKE (Methods) in reanalyses has weakened by ~ 6%, relative to the 1979–1988 period (black lines in Fig. 1a; both the mean and the individual reanalyses are shown, which exhibit almost identical evolution). CMIP6 models reproduce these historic downward trends and by the end of this century EKE is projected to decline by ~ 25% (red line). In fact, all individual CMIP6 models analyzed here have downward trends in EKE over 1979-2020 (red bars in Fig. 1b), and the MMM trend ( − 161 Jm−2yr−1 with standard deviation of 55 Jm−2yr−1 across the models) is close to the reanalyses trends ( − 147 Jm−2yr−1 with standard deviation of 46 Jm−2yr−1 across the reanalyses; black line in Fig. 1b); 61% of the CMIP6 models simulate an EKE trends that is stronger than in reanalyses.
a Evolution of EKE, relative to the 1980–1999 period, in reanalyses mean (black) and CMIP6 mean (red). Thin lines show the evolution of individual reanalyses and shading the evolution across models. b The occurrence frequency (in percentage) of the 1979–2020 trends in EKE across CMIP6 (red bars) and CMIP5 (blue bars) models. The black vertical line shows the mean reanalyses trend and gray shading its 95% confidence interval, based on a Student’s t distribution.
In contrast, most trends in CMIP5 models are smaller than in CMIP6 or reanalyses with a MMM trend of − 45 Jm−2yr−1 (blue bars in Fig. 1b); similar results are evident when using a larger ensemble size in CMIP5/6 class single-model large ensembles (Supplementary Figs. 1–2). The CMIP6 and CMIP5 distributions are statistically significantly different based on two-sample Kolmogorov-Smirnov and Student t-tests with p-values smaller than 0.05. In fact, only 8% of the CMIP5 models (2 out of 24 models) exhibit a negative trend as large as in the reanalysis19 (most models do not capture the minimum magnitude edge of the trends’ uncertainty as shown with the gray shading). The larger storm track weakening in CMIP6, relative to CMIP5, is also evident when limiting the comparison to 1979–2005 for which both model generations use historically observed forcing (Supplementary Fig. 3), and in the projected storm tracks changes by the end of this century10,23.
Detection-attribution analysis
Next we quantify to what extent the reanalysis trend could be attributed to anthropogenic emissions. To this end, we first conduct a detection analysis to assess the year that the reanalysis EKE trend emerges out of the internal variability, and thus could be explained only by the presence of external forcings. This is done using a signal-to-noise ratio (SNR) approach3,14,17,24 (Methods). Here the signal is the reanalysis trend from 1979 to each year (ranging from 1995 to 2020), and the noise is the standard deviation (s.d.) of all trends over the same number of years that could arise from internal variability. The latter is estimated from long pre-industrial control runs (Methods), and well captures the noise estimated from reanalyses (Supplementary Fig. 4). The time of emergence is defined as the year when the signal exceeds 2 s.d. of the internal variability (∣SNR∣ > 2).
We find that around 2005 the reanalysis trend emerged from the internal variability (black line in Fig. 2a), which stresses the importance of external forcings in the recent EKE weakening; internal variability alone, as represented by the models, cannot explain the EKE trends. Repeating the SNR analysis only for CMIP6 simulations in recent decades reveals a similar behavior, where around 2005 the MMM EKE trend emerged from the internal variability (red line in Fig. 2a); the CMIP5 MMM EKE trend, on the other hand, is not detectable over the historic period. Note that in spite of the temporary increase in EKE in reanalyses around 2018 (Fig. 1a), which likely stems from internal variability (since it is not evident in the MMM), the SNR not only remains above the significant threshold, but it is also projected to continue to decline in coming years (Supplementary Fig. 5).
a Signal-to-noise ratio (SNR) and (b) Fractional Attributable Risk (FAR) analyses to the JJA NH EKE trends (from 1979 to a given year) in reanalyses (black lines) and CMIP6 mean (red lines). Shadings show s.d. of SNR and FAR values (Methods). The horizontal blue line marks a signal-to-noise ratio of −2. The evolution has been smoothed with a 3-year running mean for plotting purposes.
Next, we elucidate whether the role of external forcings in weakening the EKE stems from natural or anthropogenic forcings. This is done using a Fractional Attributable Risks (FAR) approach14,25, where we calculate, for each year up to 2014 (Methods), the reanalysis trend since 1979. We then estimate the probability of having such a trend across CMIP6 models (as they are able to capture the reanalysis trend) in simulations with (PAE) and without (PNAT) anthropogenic emissions. FAR is then calculated as 1 − PNAT/PAE (Methods) (Fig. 2b). First, by 2014, the FAR of the reanalysis EKE trend reached a value of ~ 0.96 ± 0.08 (black line) indicating that we have more than 95% confidence that the trend can be attributed to anthropogenic emissions. Second, to assess whether models adequately capture the human influence on EKE, we repeat our FAR analysis but now use the trend from each CMIP6 simulation, instead of the reanalysis trend. By 2014, the MMM shows a FAR value of ~ 0.9 (red line), most models show a FAR between 0.76 and 1 ( ± s.d., red shading), and the reanalysis falls within the model spread. CMIP6 models thus adequately capture the observed EKE weakening in recent decades, but only when including human emissions.
Physical processes behind storm track weakening
What are the underlying dynamical processes by which anthropogenic emissions have weakened boreal summer storm tracks? While previous studies focused on the mechanism underlying the observed storm track weakening18,20, here we focus on the storm tracks changes in the MMM to understand the mechanisms underlying the forced response of the storm tracks to anthropogenic emissions26,27 (i.e., averaging out the internal variability/different models’ configurations). Since mid-latitude storm tracks arise from baroclinic instability (a processes by which atmospheric perturbations, such as storms, extract potential energy from the mean flow), we address this question by examining the maximum growth rate of atmospheric waves, calculated using a normal mode instability analysis (Methods). The growth rate represents the extraction of energy by the eddies (e.g., weather systems) from the mean flow, and thus enables us to link changes in the storm tracks to changes in the mean state (captured by the mean zonal wind, static stability and tropopause height, Methods).
We find that trends in the 1979–2020 growth rate adequately capture the EKE trends across CMIP6 models (r = 0.76, Fig. 3a), giving confidence to further analyze the growth rate to understand the processes behind the weakening storms. Decomposing the growth rate trends into the relative contributions from changes in the mean state (Methods) reveals that zonal wind changes are mostly responsible for the recent weakening of the growth rate, and thus of EKE (Fig. 3b); changes in static stability and tropopause height have only minor contributions to the growth rate and EKE weakening. Although we focus on the MMM forced response to anthropogenic emissions, we find similar changes in reanalyses with weakening zonal winds the dominant factor behind weakening growth rate (Supplementary Fig. 6); MERRA2 also shows large contributions from changes in static stability and tropopause height due to a much larger upper-level vs. lower-level warming relative to the other reanalyses (Supplementary Fig. 7), which questions the results from MERRA2. Note, that the human-induced changes in the growth rate due to static stability/tropopause height are small, and thus internal variability could result in opposite impacts of these processes in reanalyses relative to the MMM.
a Probability density plot of the 1979–2020 trends in eddy growth rate plotted against the 1979–2020 EKE trends across CMIP6 models. Correlation appears in the upper left corner. b Relative contribution to the growth rate trends from the mean zonal wind (U), static stability (S2) and tropopause height (H). Error bars show the 95% confidence interval based on a Student’s t-distribution. c CMIP6 MMM 1979-2020 trends in JJA U (10−2 ms−1yr−1). Black contours show the 1980–1999 zonal wind climatology (with maximum value of 20 ms−1 and spacing of 5 ms−1) and black dots indicate regions where at least two thirds of the models agree on the sign of trends. d The 1979–2020 trends in the meridional temperature difference (ΔyT) plotted against the EKE trends in CMIP6 models (probability density contours); correlation appear in the upper left corner. Green and black dots show the trends in CMIP5 and in the mean reanalyses, respectively. In (a, d) contours show the two-dimensional probability density function of the trends in CMIP6 models, estimated by fitting a kernel distribution (the area under each distribution is one).
Examining the latitude-pressure distribution of the recent trends in the zonal mean zonal wind in the CMIP6 MMM shows a robust weakening over most of the mid-latitudes at upper levels, especially at the jet’s core and its equatorward flank, and a smaller strengthening over its poleward flank (Fig. 3c). The larger weakening in the zonal mean zonal wind at upper levels, as compared to lower levels, acts to decrease the vertical wind shear (which is also evident in reanalyses, Supplementary Fig. 8) and thus the baroclinicity and the eddy growth rate. Indeed, the 1979–2020 trends in meridional temperature gradient (difference in the zonal mean temperature between 60 and 90N and 10 and 40N at 500 mb), which is directly linked to wind shear, are negatively correlated with the EKE trends across CMIP6 models (r = − 0.63, Fig. 3d). This suggests that the larger human-induced warming at high latitudes, relative to lower latitudes (Supplementary Fig. 9), and the associated reduction in wind shear, have weakened the storm tracks over recent decades. Similar changes in the vertical wind shear and temperature gradient are projected to occur by the end of this century, consistent with the projected further weakening of EKE (Supplementary Figs. 10, 11). In addition, consistent with the improved representation of storm tracks trends (Fig. 1b), CMIP6 models also better capture the reanalysis trends in meridional temperature gradient, as compared to CMIP5 models (compare green and black dots in Fig. 3d); most CMIP5 models show meridional temperature gradient trends smaller than in reanalysis. The above analysis thus supports previous studies highlighting the importance of changes in the meridional temperature gradient in weakening of the mid-latitude storm tracks18,20; such changes in temperature might not be related to sea-ice loss, which was argued to have a relatively small impact on the historic EKE weakening21.
Lastly, as discussed above, high latitude warming could weaken the zonal mean wind shear (following thermal wind balance) and thus EKE. In addition, eddies could affect the mean flow via eddy feedbacks. To examine this, we calculate the 1979–2020 trends in the conversion of EKE to mean kinetic energy (MKE) in the Lorenz energy cycle28,29 (Methods). Consistent with the overall reduction in EKE and the temperature gradient, the EKE-MKE conversion has also weakened over recent decades, especially at upper levels at mid-latitudes (Supplementary Fig. 12). This eddy feedback further reduces the zonal wind shear, thereby further contributing to reduce the growth rate and EKE.
The CMIP6-CMIP5 discrepancy
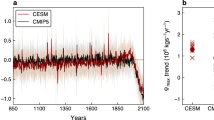
Why is there a much stronger storm track weakening signal in CMIP6 models as compared to CMIP5 models? To answer this question we first elucidate whether the weaker EKE trends in CMIP5, relative to CMIP6, stems from the different models’ configurations or from the different forcings (or a combination of both). Specifically, we compare the mid-latitude EKE trends across three large ensembles of model simulations using the Community Earth System Model (CESM). The first two ensembles use CESM versions 1 (CESM1) and 2 (CESM2), which are integrated under the CMIP5 and CMIP6 forcings, respectively (Methods). Similar to the EKE trends in CMIP6 versus CMIP5 (Fig. 1b), CESM2 also exhibits larger 1979-2014 EKE trends ( − 1.3 × 103 Jm−2yr−1) than CESM1 ( − 400 Jm−2yr−1) (Fig. 4a). Note that in both CESM2 and CESM1 the EKE is calculated as deviations from monthly mean (Methods), which results in different magnitude of EKE trends, relative to the EKE trends in Fig. 1b. Nevertheless, also here CESM2 better captures the reanalyses EKE trends, relative to CESM1 (Supplementary Figs. 1–2).
a The 1979–2014 trends in EKE in the mean of CESM1 (blue), CESM2 (red) and CESM2 integrated under CMIP5 forcings (gray). b The relative contribution of aerosol (AER), greenhouse gases (GHG) and biomass burning (BMB) emissions to the 1979–2014 trends in EKE in the mean of CESM1 (blue) and CESM2 (red). c The 1979–2014 trends in zonal mean biomass burning at each latitude in CMIP5 (blue) and CMIP6 (red). d The 1979–2014 trends in net surface shortwave flux in the mean of CESM1 (blue), CESM2 (red) and ERA5 (gray), and, the relative contribution of aerosol (AER), greenhouse gases (GHG) and biomass burning (BMB) emissions to the trends. Error bars and shadings show the 95% confidence interval based on a Student’s t-distribution.
In the third ensemble, CESM2 is integrated under CMIP5 forcings (CESM2-CMIP5, Methods), allowing us to assess the role of the different forcings in CMIP6 and CMIP5 in the different EKE trends. We find that the EKE trends in CESM2-CMIP5 ( − 680 Jm−2yr−1) are considerably reduced, relative to the EKE trends in CESM2, and show similar magnitude to the EKE trends in CESM1. We thus conclude that the different forcings used in CMIP6 vs. CMIP5 could explain most ( ~ 70%) of the larger EKE trends in CESM2, relative to CESM1. A smaller fraction can be attributed to the different models’ configurations, which were argued to affect the climatology and changes in different climate variables30,31.
To isolate the forcing agent responsible for the different EKE trends in CESM1 and CESM2 we next exploit two sets of large ensembles of CESM attribution simulations. In the first, the CESM1 is integrated using all CMIP5 forcing agents except for one, which is kept constant at 1920 values (CESM1-EB, Methods). The contribution of each forcing agent to the EKE trend in CESM1 is estimated as the difference between the CESM1 and the CESM1-EB trends. In the second set of ensembles, the CESM2 is integrated with the time evolution of only a single forcing agent, while all others are kept constant at 1850 values (CESM2-SF, Methods); the EKE trends in these simulations provide the contribution of each forcing agent to the CESM2 EKE trends.
First, we find that in both CESM1 and CESM2 the EKE trend is attributed to aerosols and greenhouse gases emissions (Fig. 4b). Note that the slightly reduced contributions of these forcings agents in CESM2, relative to CESM1, might be due to the different attribution techniques (everything-but-one vs. only-one forcing, Supplementary Fig. 13); the impact of the different attribution techniques might be sensitive to the targeted forcing agent (e.g., here the different techniques are examined on the aerosol forcing), and, different models might have different sensitivities to such attribution techniques31. Second, in CESM2, the sum of the individual contributions do not account for the full EKE trends, suggesting a role of natural forcings or non-linear interactions between the different forcing agents. Third, and most importantly, the larger EKE trends in CESM2, relative to CESM1, stems from biomass burning emissions. In CESM1, biomass burning emissions act to considerably mitigate the EKE trend induced by the other forcings, while in CESM2 they have negligible influence.
Examining the 1979–2014 applied biomass burning emissions trends (Fig. 4c) reveals that while in CMIP5 biomass burning emissions decreased at mid-latitudes (between 40 and 60N), in CMIP6 the emissions increased at mid-high latitudes (between 55 and 65N) (the larger decline in biomass burning emissions in CMIP5, relative to CMIP6, is also evident over the historic CMIP5 1979–2005 period alone). These different trends, over different latitudes, could directly and/or indirectly (via aerosol-cloud interactions) impact solar radiation changes in recent decades32, and thus affect, for example, the meridional temperature gradient and the EKE trends. Thus, to assess which biomass burning changes are more realistic, we next compare the surface solar radiation trends in CESM1 and CESM2 with the trends in the reanalysis. Similar to the EKE trends, while the CESM2 and the reanalysis show similar robust (and positive) 1979–2014 trends in mid-high-latitude (averaged between 50 and 70N) net surface solar radiation, CESM1 exhibits a negligible trend due to the mitigating effect of biomass burning emissions (Fig. 4d). Not only that similar results are found in CMIP5 and CMIP6 models (Supplementary Fig. 14), but also the EKE trends in CMIP5 models exhibit a statistical significant correlation with net surface solar radiation trends (r = − 0.61), while CMIP6 model do not (r = − 0.14). Based on the above CESM analysis, we suggest that the underestimated EKE signal in most CMIP5 models might stem from inaccurate changes in biomass burning forcings.
Note that the recently found artificial impacts of biomass burning interannual variability on the changes in Northern Hemisphere mid-high latitude climate in CESM232 cannot explain the larger EKE trends in CESM2 relative to CESM1, but they do seem to generate a slightly more pronounced EKE weakening (Supplementary Fig. 15). Lastly, while it is conceivable that the larger climate sensitivity in CMIP6 models, relative to CMIP5 models, could also result in the different EKE weakening trends, the EKE discrepancy remains even when normalizing the EKE trends by surface warming, and CMIP6 models still better capture the reanalyses trend, suggesting that the different surface warming in CMIP6 and in CMIP5 is not likely the source for the EKE discrepancy (Supplementary Fig. 16).
Discussion
Our analyses provide evidence that anthropogenic emissions, via enhanced warming of the high latitudes, relative to lower latitudes, has already weakened the mid-latitude summer storm tracks. The consistency between reanalyses and CMIP6 models, in terms of trends and underlying dynamical processes, provides confidence in our findings and in model projections of the mid-latitude climate. The latest IPCC report states ‘low confidence’ in the potential role of human activity on historic boreal mid-latitude storm tracks changes. A FAR of ~ 0.96 ± 0.08, as reported here for weakening of EKE, implies more than 95% chance (or ‘extremely likely’ in the IPCC lexicon) that the storm tracks weakening is due to anthropogenic emissions.
Our analyses of the underlying physical processes clearly link the observed and modeled changes to summertime high latitude warming, relative to lower latitudes. We show that these warming trends in reanalysis are adequately captured in CMIP6 models but not in most CMIP5 models. This discrepancy between CMIP5 and CMIP6 models propagates in the associated weakening of mid-latitude summer storm tracks with CMIP6 models having much more pronounced weakening. Using a set of CESM ensembles, our results suggest that in CMIP5 models, biased biomass burning forcing at high latitudes might counteract, and thereby cancel most of the aerosol and greenhouse gases induced EKE weakening. This stresses the importance of further quantifying the role of biomass burning emissions in shortwave radiation and storm track changes in observations and other climate models (besides CESM), and of accurately incorporating these emissions in climate models to adequately capture recent climate changes in the Northern Hemisphere.
The dynamical changes reported here could have important implications for weather variability and extremes in regions affected by the storm tracks. For example, western Europe, located at the exit region of the North Atlantic storm track, has seen a very strong increase in hot-dry extremes, at least three times faster than other mid-latitude regions33, and, dynamical changes are thought to play a role in this amplified trend34. In summer, synoptic storms have a cooling effect on continental temperatures by bringing relatively moist, cool and cloudy weather conditions from the oceans to continents. Low cyclone activity (i.e., low EKE) implies that cool maritime air masses become less frequent, with less cloud cover over land, creating favorable conditions for the buildup of heat and drought over continents. Weakening storm tracks could also lead to reductions in soil moisture, which might feedback again on the large scale circulation35. This hypothetical mechanism would be especially relevant for the continental west coasts including Europe, which has experienced extreme droughts in recent warm seasons36,37,38. Studies based on observations and climate model analyses indeed show that weakening storm tracks favor hot-and-dry extremes over the continents19,36,39. Moreover, weakening storm tracks could potentially favor more-persistent weather conditions40,41, which could exacerbate impacts from both hot-dry extremes and rainfall extremes, with persistent rainfall extremes leading to flood risks42. Thus, the human influence on summertime storm tracks found here could cascade to regional extreme weather events over the continents in the Northern Hemisphere.
Methods
Mid-latitude storm tracks
The boreal summer storm tracks intensity is defined, following previous studies18, as the tropospheric (integrated between 850 and 300 mb) June-August transient eddy kinetic energy, \({{{\rm{EKE}}}}=\frac{1}{g}\int{u}^{{* }^{2}}+{v}^{{* }^{2}}dp\), where g is gravity, u and v are the zonal and meridional winds, respectively, p is pressure and asterisks denote eddy terms, calculated using a bandpass filter of 2.5-6 days. The EKE is averaged over the mid-latitudes (zonal mean and between 30 and 60N) since its forced weakening is evident across most of the mid-latitudes and throughout the troposphere (Supplementary Figs. 17, 18); reanalyses also exhibit an EKE weakening at higher latitudes that is not evident in the MMM, and thus might stem from internal variability. Prior to spatially averaging the EKE all datasets were interpolated to the same grid.
Reanalyses
To investigate the recent changes in boreal summer storm tracks we examine monthly and 6-hourly instantaneous data in four different reanalyses: ERA543, JRA-5544, NCEP245 and MERRA246. By assimilating surface and air observations in general circulation models, reanalyses provide the best estimate of the state of the atmosphere in recent decades.
CMIP6
We also examine monthly and daily averaged data in CMIP647 models (Supplementary Table 1) using the ‘r1i1p1f1’ member from the following four experiments: historical (through 2014), future scenario SSP5-8.5 (through 2100), historical with only natural forcings (through 2014; hist-nat), and pre-industrial control run (with constant 1850 forcings, which thus comprises only the internal variability of the system). We use only one member from each model in order to weigh all models equally. To evaluate the internal variability of the storm tracks trends we use the last 200 years of the pre-industrial run from each model.
CMIP5
Monthly and daily averaged data from CMIP5 models48 (Supplementary Table 2) are analyzed using the ‘r1i1p1’ member from the historical (through 2005) and future scenario RCP8.5 (through 2100).
CESM
To elucidate the source of the different EKE trends in CMIP5 and CMIP6 models we exploit a set of large ensembles of model simulations using the CESM model. Specifically, to compare the EKE trends in CMIP5 and CMIP6 using CESM we examine the 40 member CESM1 large-ensemble integrated over the 1920–2100 period under the historical and RCP8.5 CMIP5 forcings49, and 40 members from the CESM2-SMBB large-ensemble integrated over the 1850–2100 period under the historical and SSP3-7.0 CMIP6 forcings50. We here use the CESM2-SMBB large-ensemble rather than the CESM2-CMIP6 ensemble for consistency with the single forcing ensemble discussed below. In addition, it was recently shown that in CESM2-CMIP6 the incorporation of different biomass burning emission sources resulted in discontinuities in the variability of these emissions that lead to artificial changes in the Northern Hemisphere climate in recent decades32,51. CESM2-SMBB thus uses a smoothed evolution of biomass burning emissions that removes these historic artificial changes.
To examine the role of the different forcings used in CMIP5 and CMIP6 in recent EKE trends we also make use of a 10-member CESM2 ensemble integrated under CMIP5 forcings52. Lastly, to isolate the forcing agent responsible for the different EKE trends in CESM1 and CESM2-SMBB we use six large ensembles of simulations (of 15–20 members each) using CESM1 (CESM1-EB) and CESM2-SMBB (CESM2-SF). In each CESM1-EB ensemble a different forcing agent (aerosol, greenhouse gases and biomass burning emissions) is held fixed, while all other forcing agents freely evolve53. If non-linear interactions between the forcing agents have relatively minor impacts on the EKE trends, then the contribution of each forcing agent to the EKE trend is assessed as the difference between the EKE trends in CESM1 (i.e., when all forcings are active) and in CESM1-EB (i.e., when all forcings agents freely evolve expect for one). In each CESM2-SF ensemble only one of the forcing agents is allowed to freely evolve, while all other forcing agents are held fixed31. Thus, the EKE trends in these simulations are used to assess the contribution of each forcing agent to the EKE trend in CESM2-SMBB, again, assuming non-linearities are not important. As discussed in the text, the use of these two different methods to estimate the relative contribution of each forcing agent on the EKE trend has only minor impact on our results (Supplementary Fig. 13). Lastly, the EKE in all CESM simulations is estimated as deviations from monthly mean, due the availability of only monthly kinetic energy data (accumulated over each model time step) in some of the above ensembles, which results in larger EKE trends relative to the bandpass filter method. Nevertheless, not only that the EKE trends in CESM1/2 capture the larger weakening in CMIP6-class vs. CMIP5-class models, but calculating the EKE trends in reanalyses as deviations from monthly mean also yields similar values as in CESM2, which are not adequately captured in CESM1 (Supplementary Figs. 1, 2).
Signal to noise ratio
The SNR approach allows us to assess whether the weakening signal of the storms emerged from the internal variability in recent decades. Specifically, the signal is defined as trends of EKE since 1979 (the first year in the reanalyses) to each year, and the noise as s.d. of all trends, of the same length as the signal, estimated from the CMIP6 preindustrial control runs of each model. The SNR is estimated as the mean of SNR values using the noise from all preindustrial runs, and its uncertainty as s.d. across the runs.
Fractional Attributional Risk
We use the FAR approach14,25 to attribute the recent weakening of boreal storm tracks to anthropogenic emissions. This is done by calculating at each year the reanalysis EKE trend (all starting at 1979), and estimating the probability of exceeding such a trend in CMIP6 models forced with (PAE, i.e., under the historical forcing) and without (PNAT, i.e., under the hist-nat forcing) anthropogenic emissions. FAR is then estimated as 1 − PNAT/PAE, which provides us with the probability of the reanalysis trend being attributed to anthropogenic emissions (e.g., a FAR of 0.75 means that there is 75% chance that a given trend is due to human activity). The FAR is estimated up to 2014, since this is the last year in the historical simulations with only natural forcings. To overcome the different number of models in the historical and hist-nat simulations, which may lead to different estimates of the internal variability of trends, the CMIP6 trend distribution around the MMM historical/hist-nat simulations is estimated by fitting a kernel distribution to the spread of trends from each preindustrial run. FAR is estimated as the mean of FAR values using all preindustrial runs, and its uncertainty as s.d. across the runs.
Linear-normal mode instability analysis
To investigate via which mechanism anthropogenic emissions weakened the storm tracks in recent decades we follow previous studies17,54,55,56 and conduct a linear-normal mode instability analysis using the linearized (about a zonal mean state; denoted by overbars) quasi-geostrophic equations, which can be written for simplicity as follows,
where q is the quasi-geostrophic potential vorticity, \({q}^{{\prime} }={\nabla }^{2}{\psi }^{{\prime} }+\Gamma {\psi }^{{\prime} }\), primes denotes deviations from zonal mean, where \({u}^{{\prime} }=-\frac{\partial {\psi }^{{\prime} }}{\partial y}\) and \({v}^{{\prime} }=\frac{\partial {\psi }^{{\prime} }}{\partial x}\), \(\Gamma =\frac{\partial }{\partial p}\frac{{f}^{2}}{{S}^{2}}\frac{\partial }{\partial p}\), \({S}^{2}=-\frac{1}{\overline{\rho }\overline{\theta }}\frac{\partial \overline{\theta }}{\partial p}\) is static stability, θ is potential temperature, ρ is density, \(\frac{\partial \overline{q}}{\partial y}=\beta -\Gamma \overline{u}\) is the meridional gradient of mean quasi-geostrophic potential vorticity, β is the meridional derivative of the Coriolis parameter (f) and Hp is the tropopause height (defined, following the WMO, as the lowest level where the vertical temperature gradient crosses the 2 km−1 value, and stays on average below this value in higher levels within 2 km). By assuming a plane wave solution of the form, \({\psi }^{{\prime} }={{{\rm{Re}}}}\hat{{\psi }^{{\prime} }}(p){e}^{i(kx-\omega t)}\), the above equation can be written as an eigenvalue problem, where \(\hat{{\psi }^{{\prime} }}\) is the normal modes (eigenvectors), ω is the frequency (eigenvalues) and k is the zonal wavenumber. The zonal mean fields (mean zonal wind, temperature and tropopause height, i.e., the input parameters) are averaged over the mid-latitudes (30−60N), and are only a function of height. The vertical eigenvalue problem is solved for each summer, and we examine the trends of the fastest growth rate. Finally, to examine the relative contribution of each zonal mean field in the growth rate changes, we re-solve the above eigenvalue problem but allow only one of the input parameters (the mean fields) to change over the 1979–2020 period.
EKE to MKE conversion
The conversion from EKE to MKE is calculated, following previous work29, using both transient and stationary eddies as follows,
where square brackets denote monthly means and asterisks deviations therefrom and w is vertical velocity.
Data availability
The data used in the manuscript is publicly available for CMIP6 data (https://esgf-node.llnl.gov/projects/cmip6/), CMIP5 data (https://esgf-node.llnl.gov/projects/cmip5/), JRA55 and MERRA2 (https://rda.ucar.edu/), ERA5 (https://www.ecmwf.int), NCEP (https://psl.noaa.gov/) and CESM (https://www.earthsystemgrid.org/).
Code availability
The code for the normal-mode instability analysis is available at https://doi.org/10.5281/zenodo.6434217.
References
Masson-Delmotte, V. et al. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge Univ. Press, pp. 2391, 2021).
Bilbao, R. A. F., Gregory, J. M., Bouttes, N., Palmer, M. D. & Stott, P. Attribution of ocean temperature change to anthropogenic and natural forcings using the temporal, vertical and geographical structure. Clim. Dyn. 53, 5389–5413 (2019).
Santer, B. D. et al. Human and natural influences on the changing thermal structure of the atmosphere. Proc. Natl. Acad. Sci. USA 110, 17235–17240 (2013).
Santer, B. D. et al. Contributions of Anthropogenic and Natural Forcing to Recent Tropopause Height Changes. Science 301, 479–483 (2003).
Mueller, B. L., Gillett, N. P., Monahan, A. H. & Zwiers, F. W. Attribution of Arctic Sea Ice Decline from 1953 to 2012 to Influences from Natural, Greenhouse Gas, and Anthropogenic Aerosol Forcing. J. Clim. 31, 7771–7787 (2018).
Jones, G. S., Stott, P. A. & Christidis, N. Attribution of observed historical near-surface temperature variations to anthropogenic and natural causes using CMIP5 simulations. J. Geophys. Res. 118, 4001–4024 (2013).
Vallis, G. K., Zurita-Gotor, P., Cairns, C. & Kidston, J. Response of the large-scale structure of the atmosphere to global warming. Q. J. R. Meteorol. Soc. 141, 1479–1501 (2015).
Chang, E. K. M., Guo, Y. & Xia, X. CMIP5 multimodel ensemble projection of storm track change under global warming. J. Geophys. Res. 117, D23118 (2012).
Harvey, B. J., Shaffrey, L. C. & Woollings, T. J. Equator-to-pole temperature differences and the extra-tropical storm track responses of the CMIP5 climate models. Clim. Dyn. 43, 1171–1182 (2014).
Harvey, B. J., Cook, P., Shaffrey, L. C. & Schiemann, R. The Response of the Northern Hemisphere Storm Tracks and Jet Streams to Climate Change in the CMIP3, CMIP5, and CMIP6 Climate Models. J. Geophys. Res. 125, e32701 (2020).
Dong, B. & Sutton, R. T. Recent Trends in Summer Atmospheric Circulation in the North Atlantic/European Region: Is There a Role for Anthropogenic Aerosols? J. Clim. 34, 6777–6795 (2021).
Dong, B., Sutton, R. T., Shaffrey, L. & Harvey, B. Recent decadal weakening of the summer Eurasian westerly jet attributable to anthropogenic aerosol emissions. Nat. Commun. 13, 1148 (2022).
Grise, K. M. et al. Recent Tropical Expansion: Natural Variability or Forced Response? J. Clim. 32, 1551–1571 (2019).
Chemke, R. & Yuval, J. Human induced weakening of the Northern Hemisphere tropical circulation. Nature 617, 529–532 (2023).
Shepherd, T. G. Atmospheric circulation as a source of uncertainty in climate change projections. Nat. Geosci. 7, 703–708 (2014).
Chemke, R. & Polvani, L. M. Linking midlatitudes eddy heat flux trends and polar amplification. npj Clim. Atmos. Sci. 3, 8 (2020).
Chemke, R., Ming, Y. & Yuval, J. The intensification of winter mid-latitude storm tracks in the Southern Hemisphere. Nat. Clim. Change 12, 553–557 (2022).
Coumou, D., Lehmann, J. & Beckmann, J. The weakening summer circulation in the Northern Hemisphere mid-latitudes. Science 348, 324–327 (2015).
Chang, E. K. M., Ma, C., Zheng, C. & Yau, A. M. W. Observed and projected decrease in Northern Hemisphere extratropical cyclone activity in summer and its impacts on maximum temperature. Geophys. Res. Lett. 43, 2200–2208 (2016).
Gertler, C. G. & O’Gorman, P. A. Changing available energy for extratropical cyclones and associated convection in Northern Hemisphere summer. Proc. Natl. Acad. Sci. USA 116, 4105–4110 (2019).
Kang, J. M., Shaw, T. A. & Sun, L. Arctic Sea Ice Loss Weakens Northern Hemisphere Summertime Storminess but Not Until the Late 21st Century. Geophys. Res. Lett. 50, e2022GL102301 (2023).
Coumou, D., Di Capua, G., Vavrus, S., Wang, L. & Wang, S. The influence of Arctic amplification on mid-latitude summer circulation. Nat. Commun. 9, 2959 (2018).
Chang, E. K. M., Yau, A. M. W. & Zhang, R. Finding Storm Track Activity Metrics That Are Highly Correlated with Weather Impacts. Part II: Estimating Precipitation Change Associated with Projected Storm Track Change over Europe. J. Clim. 35, 2423–2440 (2022).
Hawkins, E. & Sutton, R. Time of emergence of climate signals. Geophys. Res. Lett. 39, L01702 (2012).
Stott, P. A. et al. Attribution of extreme weather and climate-related events. WIREs Clim. Change 7, 23–41 (2016).
Deser, C., Knutti, R., Solomon, S. & Phillips, A. S. Communication of the role of natural variability in future North American climate. Nat. Clim. Change 2, 775–779 (2012).
Santer, B. D. et al. Identifying human influences on atmospheric temperature. Proc. Natl. Acad. Sci. USA 110, 26–33 (2013).
Lorenz, E. N. Available potential energy and the maintenance of the general circulation. Tellus 7, 157–167 (1955).
Peixoto, J. P. & Oort, A. H.Physics of Climate (American Institute of Physics, 1992).
DuVivier, A. K. et al. Arctic and Antarctic Sea Ice Mean State in the Community Earth System Model Version 2 and the Influence of Atmospheric Chemistry. J. Geophys. Res. 125, e2019JC015934 (2020).
Simpson, I. R. et al. The CESM2 Single-Forcing Large Ensemble and Comparison to CESM1: Implications for Experimental Design. J. Clim. 36, 5687–5711 (2023).
Fasullo, J. T. et al. Spurious Late Historical-Era Warming in CESM2 Driven by Prescribed Biomass Burning Emissions. Geophys. Res. Lett. 49, e97420 (2022).
Rousi, E., Kornhuber, K., Beobide-Arsuaga, G., Luo, F. & Coumou, D. Accelerated western European heatwave trends linked to more-persistent double jets over Eurasia. Nat. Commun. 13, 3851 (2022).
Vautard, R. et al. Heat extremes in Western Europe increasing faster than simulated due to atmospheric circulation trends. Nat. Commun. 14, 6803 (2023).
Teng, H. & Branstator, G. Amplification of waveguide teleconnections in the boreal summer. Curr. Clim. Change Rep. 5, 421–432 (2019).
Ionita, M., Nagavciuc, V., Kumar, R. & Rakovec, O. On the curious case of the recent decade, mid-spring precipitation deficit in central Europe. npj Clim. Atmos. Sci. 3, 49 (2020).
Büntgen, U. et al. Recent European drought extremes beyond Common Era background variability. Nat. Geosci. 14, 190–196 (2021).
Ionita, M., Dima, M., Nagavciuc, V., Scholz, P. & Lohmann, G. Past megadroughts in central Europe were longer, more severe and less warm than modern droughts. Commun. Earth Environ. 2, 61 (2021).
Lehmann, J. & Coumou, D. The influence of mid-latitude storm tracks on hot, cold, dry and wet extremes. Sci. Rep. 5, 17491 (2015).
Pfleiderer, P. & Coumou, D. Quantification of temperature persistence over the Northern Hemisphere land-area. Clim. Dyn. 51, 627–637 (2018).
Pfleiderer, P., Schleussner, C., Kornhuber, K. & Coumou, D. Summer weather becomes more persistent in a 2 ∘C world. Nat. Clim. Change 9, 666–671 (2019).
Kahraman, A., Kendon, E. J., Chan, S. C. & Fowler, H. J. Quasi-Stationary Intense Rainstorms Spread Across Europe Under Climate Change. Geophys. Res. Lett. 48, e92361 (2021).
Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049 (2020).
Kobayashi, S. et al. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteor. Soc. Japan 93, 5–48 (2015).
Kanamitsu, M. et al. NCEP-DOE AMIP-II reanalysis (R-2). Bull. Am. Meteor. Soc. 83, 1631–1643 (2002).
Gelaro, R. et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 30, 5419–5454 (2017).
Eyring, V. et al. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteor. Soc. 93, 485–498 (2012).
Kay, J. E. et al. The Community Earth System Model (CESM) Large Ensemble Project: A Community Resource for Studying Climate Change in the Presence of Internal Climate Variability. Bull. Am. Meteor. Soc. 96, 1333–1349 (2015).
Rodgers, K. B. et al. Ubiquity of human-induced changes in climate variability. Earth Syst. Dyn. 12, 1393–1411 (2021).
DeRepentigny, P. et al. Enhanced simulated early 21st century Arctic sea ice loss due to CMIP6 biomass burning emissions. Sci. Adv. 8, eabo2405 (2022).
Holland, M. M. et al. New model ensemble reveals how forcing uncertainty and model structure alter climate simulated across CMIP generations of the Community Earth System Model. Geosci. Model Dev. 17, 1585–1602 (2024).
Deser, C. et al. Isolating the Evolving Contributions of Anthropogenic Aerosols and Greenhouse Gases: A New CESM1 Large Ensemble Community Resource. J. Clim. 33, 7835–7858 (2020).
Chemke, R. & Ming, Y. Large atmospheric waves will get stronger, while small waves will get weaker by the end of the 21st century. Geophys. Res. Lett. 47, e2020GL090441 (2020).
Chemke, R., Zanna, L., Orbe, C., Sentman, L. T. & Polvani, L. M. The Future Intensification of the North Atlantic Winter Storm Track: The Key Role of Dynamic Ocean Coupling. J. Clim. 35, 2407–2421 (2022).
Chemke, R. The future poleward shift of Southern Hemisphere summer mid-latitude storm tracks stems from ocean coupling. Nat. Commun. 13, 1730 (2022).
Acknowledgements
R.C. is grateful to the support by the Willner Family Leadership Institute for the Weizmann Institute of Science. D.C. is grateful to the funding from the European Union’s Horizon 2020 Research and Innovation Programme under Grants 101003469 and 101137656.
Author information
Authors and Affiliations
Contributions
R.C. analyzed the data and together with D.C. discussed and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chemke, R., Coumou, D. Human influence on the recent weakening of storm tracks in boreal summer. npj Clim Atmos Sci 7, 86 (2024). https://doi.org/10.1038/s41612-024-00640-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-024-00640-2
- Springer Nature Limited