Entropy of amorphous ice

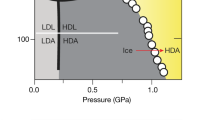
Abstract

THE configurational entropies of amorphous solids reflect certain aspects of their structures, in particular the numbers of accessible molecular configurations. The configurational entropy of vitreous silica has been estimated theoretically¹ as no more than 5.8 J K⁻¹ mol⁻¹, which agrees reasonably with experiment. That of low-density amorphous ice has been estimated theoretically² as ∼6.3 J K⁻¹ mol⁻¹ more than that of ice Ih, using a model that assumes a continuous random network of hydrogen bonds. This value corresponds to ∼ 2.1 more configurations per molecule than in ice Ih, and seems consistent with the result for vitreous silica¹. In principle, these entropies can be obtained from the change of heat capacity from the glass to the liquid and the entropy of freezing of the liquid at equilibrium, but such measurements have not proved possible because the liquid generally crystallizes too quickly. Here we show that the entropies can be estimated approxi-mately by another method: from the thermodynamics of the transformations of, for example, both ice Ih³ and low-density amorphous ice⁴ to high-density amorphous ice. The entropy of high-density amorphous ice relative to that of ice Ih is estimated as 2± 1 J K⁻¹ mol⁻¹ and that of high-density relative to low-density amorphous ice is estimated as 1 ±0.5 J K⁻¹ mol⁻¹. The entropy of low-density amorphous ice relative to ice Ih is therefore ∼ 1 J K⁻¹ mol⁻¹. The earlier estimates^2,5 of this quantity are there-fore several times too high. These low values limit the amount of disorder that can be present in the amorphous phases.