Abstract
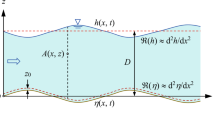
Sea-waves are understood more easily if they are considered to move with constant velocity and without changing shape. A convenient mathematical technique is to imagine that these waves can be arrested in space and analysed as for flowing streams with a steady wave-like surface deformation. Hitherto, this technique has been used almost exclusively to study progressive surface waves. For depths as great as 45 m, such wave-like deformations occur on the sea surface as a weakly coupled mirror-image of sandwaves on the seabed. By assuming that these surface deformations are real arrested progressive waves and not merely analogous, we now show that sand-dunes are related empirically by a small-amplitude surface wave dispersion equation. Furthermore, finite-amplitude wave theory (that is, steepest wave theory) is related to the steepest dunes on a stream bed where previously, for want of a better theory, steepest dune wavelengths have been explained in terms of fluid turbulence. In particular, if the dune wavelengths associated here with Gerstner's finite amplitude theory are combined in a manner similar to a beat effect, the predicted wavelengths are in good agreement with the lengths of marine sandwaves.
Similar content being viewed by others
References
Allen, J. R. L. Physical Processes of Sedimentation (Allen & Unwin, London, 1970).
Kennedy, J. F. J. Fluid Mech. 16, 521–544 (1963).
Milne-Thomson, L. M. Theoretical Hydrodynamics (Macmillan, London, 1968).
Lamb, H. Infinitesimal Calculus (Cambridge University Press, 1919).
Parker, G. J. Hydraul. Div. Am. Soc. civ. Engrs 101, (HY2) 211–221 (1975).
Yalin, M. S. Mechanics of Sediment Transport (Pergamon, Oxford, 1977).
Sundborg, A. Geogr. Annlr 38, 126–316 (1956).
Guy, H. P. et al. Geol. Surv. Prof. Pap. 462-I (U.S. Print Office, Washington DC, 1966).
Stein, R. A. J. Geophys. Res. 70, 1831–1842 (1965).
Simons, D. B. et al. Geol. Surv. Water-Supply Pap. 1498A (U.S. Print Office, Washington DC, 1961).
McLeish et al. Mar. Geol. (submitted).
Allen, J. R. L. Sedimentology 27, 317–324 (1980).
Ippen, A. T. Estuary and Coastline Hydrodynamics (McGraw-Hill, New York, 1966),
Bouma, A. H. et al. Mar. Geotechnol. 2, 291–308 (1977).
Langhorne, D. N. Mar. Geol. (in the press).
Blackley, M. W. L. IOS Rep. 60, (1978).
Smith, J. & McLean, S. R. J. geophys. Res. 82, 1735–1746 (1977).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Hammond, F., Heathershaw, A. A wave theory for sandwaves in shelf-seas. Nature 293, 208–210 (1981). https://doi.org/10.1038/293208a0
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/293208a0
- Springer Nature Limited