Skip to main content
SpringerLink
Log in

Dynamic–Stochastic Modeling of Rivers Rising from Lakes

  • Published:
Water Resources Aims and scope Submit manuscript

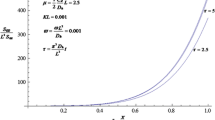
Abstract

Problems arising in modeling long-term variations in rivers rising from lakes are discussed in the context of the theory of correlation of non-Gaussian stochastic processes and with the use of Fokker–Plank–Kolmogorov equation. Numerically simulated runoff values of the Angara River rising from Lake Baikal are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. Bakanov, K.G., A Nonlinear Probabilistic Model of a Flow-Through Lake, Metody postroeniya i analiza modeli slozhnykh prirodnykh sistem (Methods of Construction and Analysis of Models for Complex Natural Systems), Vladivostok: Izd. Dal'nevost. Gos. Univ., 1986, pp. 114–129.

    Google Scholar 

  2. Ratkovich, D.Ya., Mnogoletnie Kolebaniya Rechnogo Stoka (Long-Term Fluctuations of River Runoff), Leningrad: Gidrometeoizdat, 1976.

    Google Scholar 

  3. Vodnoenergeticheskie raschety metodom Monte-Karlo (Hydraulic-Power Computations by the Monte-Carlo Method), Reznikovskii, A.Sh., Ed., Moscow: Energiya, 1969.

    Google Scholar 

  4. Tikhonov, V.I. and Mironov, M.A., Markovskie protsessy (Markov Processes), Moscow: Sovetskoe Radio, 1977.

  5. Frolov, A.V., Dinamiko-Stokhasticheskie Modeli Mnogoletnikh Kolebanii Urovnya Protochnykh Ozer (Dynamic and Stochastic Models of Long-Term Level Fluctuations in Drainage Lakes), Moscow: Nauka, 1985.

    Google Scholar 

  6. Frolov, A.V., Dynamic and Stochastic Models of Long-Term Fluctuations in Some Hydrological Processes, Vody sushi: problemy i resheniya (Continental Waters: Problems and Solutions), Moscow: Inst. Vodnykh Problem, Ross. Akad. Nauk, 1994, pp. 179–192.

    Google Scholar 

  7. Klemes, V., Distribution of Outflow From a Lake with Serially Correlated Inflow, IASH Publ., 1973, vol. 1, pp. 106–109.

    Google Scholar 

  8. Klemes, V., Watershed as Semi-infinite Storage Reservoir, J. Irrig. Drain. Div. ASCE, 1973, vol. 99, no. 4, pp. 477–491.

    Google Scholar 

  9. Klemes, V., Probability Distribution of Outflow a Linear Reservoir, J. Hydrol. (Amsterdam), 1974, vol. 21, no. 3, pp. 305–414.

    Google Scholar 

  10. Klemes, V., Physically Based Stochastic Hydrologic Analysis, Adv. Hydrosci., 1978, vol. 11, pp. 285–356.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Water Problems Institute, Russian Academy of Sciences, ul. Gubkina 3, GSP-1, Moscow, 119991, Russia

    A. V. Frolov, T. Yu. Vyruchalkina & I. V. Solomonova

Authors
  1. A. V. Frolov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Yu. Vyruchalkina
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. I. V. Solomonova
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Frolov, A.V., Vyruchalkina, T.Y. & Solomonova, I.V. Dynamic–Stochastic Modeling of Rivers Rising from Lakes. Water Resources 30, 627–631 (2003). https://doi.org/10.1023/B:WARE.0000007588.34023.a6

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/B:WARE.0000007588.34023.a6

Keywords

Search

Navigation