Theoretical and Experimental Study on the Parametrically Excited Vibration of Mass-Loaded String

Abstract

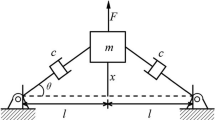
The parametrically excited lateral vibration of a mass-loaded string is investigated in this paper. Supposing that the mass at the lower end of the string is subjected to a vertical harmonic excitation and neglecting the higher-order vibration modes, the equation of motion for the mass-loaded string can be represented by a Mathieu's equation with cubic nonlinearity. Based on the stability criterion for Mathieu's equation, the critical conditions inducing parametric resonance are clarified. Theoretical analysis shows that when the natural frequency f _s of the string lateral vibration and the vertical excitation frequency f satisfy f _s= (n/2)f, n= 1, 2, 3, ..., parametric resonance occurs in the case of no damping. For a damped system, parametric resonance most likely occurs when f is close to 2f _s, and depends on the damping of the system and the vertical excitation. The critical excitation has been derived at different frequencies. If the natural frequency of the mass vertical vibration happens to be twice that of the string lateral vibration, the parametric resonance may occur due to a small disturbance. Numerical simulations show that the lateral vibration of the string does not increase infinitely at parametric resonance because the parametric excitation is self-tuned due to the coupling between the vertical and lateral vibrations. Finally, the theoretical results are supported by some experimental work.