Skip to main content
SpringerLink
Log in

A Computational Model of Fatigue Fracture of Materials

  • Published:
Materials Science Aims and scope

Abstract

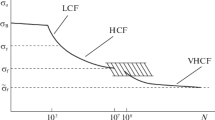
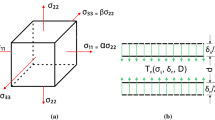
We propose a rule for the description of the accumulation of damage in materials under the conditions of cyclic straining. By using this rule, we study the processes of cyclic elastoplastic straining at the crack tip and deduce new kinetic equations of fatigue-crack propagation. It is established that the growth rate of a macrocrack in a cyclically deformed body depends not only on the parameters of loading and known strength characteristics of the material but also on the parameters taking into account the intensity of accumulation of defects and the instability of width of the hysteresis loop observed as the number of loading cycles increases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. J. Schijve, “Fatigue of structures and materials in the 20th century and the state of the art,” in: Proc. of the ECF14–2002, Vol. 3 (2002), pp. 211–262.

    Google Scholar 

  2. V. G. Troshchenko, Fatigue and Inelasticity of Metals [in Russian], Naukova Dumka, Kiev (1971).

    Google Scholar 

  3. L. E. Coffin, “A study of the effects of cycle thermal stresses in ductile metals,” Trans. ASME, No. 76, 794–807 (1954).

    Google Scholar 

  4. S. S. Manson, Thermal Stress and Low-Cycle Fatigue, McGraw-Hill, New York (1966).

    Google Scholar 

  5. V. V. Panasyuk, Limiting Equilibrium of Brittle Cracked Bodies [in Russian], Naukova Dumka, Kiev (1968).

    Google Scholar 

  6. J. R. Rice, “Mechanics of crack-tip deformation and extension by fatigue,” in: Fatigue Crack Propagations, (1967), p. 247.

  7. B. Budiansky and J. W. Hutchinson, “Analysis of closure in fatigue crack growth,” Trans. ASME, No. 45, 267–276 (1978).

    Google Scholar 

  8. V. V. Panasyuk, O. E. Andreikiv, R. O. Ritchie, and O. I. Darchuk,” Int. J. Fract., 107, No. 2, 99–115 (2001).

    Google Scholar 

  9. N. A. Makhutov, Deformation Fracture Criteria and Strength Analysis of Structural Elements [in Russian], Mashinostroenie, Moscow (1981).

    Google Scholar 

  10. O. N. Romaniv, S. Ya. Yarema, G. N. Nikiforchin, et al., Fatigue and Cyclic Crack Resistance of Structural Materials [in Russian], Naukova Dumka, Kiev (1990), Vol. 4 in: V. V. Panasyuk (editor), Fracture Mechanics and Strength of Materials. A Handbook [in Russian], Naukova Dumka, Kiev (1988–1990).

    Google Scholar 

  11. A. Ya. Krasovskii and V. V. Kalaida, Strength and Crack Resistance of Spherulitic Cast Irons [in Russian], Naukova Dumka, Kiev (1989).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Karpenko Physicomechanical Institute, Ukrainian Academy of Sciences, Lviv

    V. V. Panasyuk & V. P. Sylovanyuk

Authors
  1. V. V. Panasyuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. P. Sylovanyuk
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Panasyuk, V.V., Sylovanyuk, V.P. A Computational Model of Fatigue Fracture of Materials. Materials Science 39, 351–364 (2003). https://doi.org/10.1023/B:MASC.0000010740.79476.62

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/B:MASC.0000010740.79476.62

Keywords

Search

Navigation