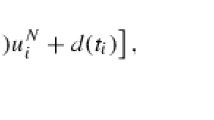Abstract
This paper is concerned with the asymptotic analysis of the trajectories of some dynamical systems built upon the gradient projection method in Hilbert spaces. For a convex function with locally Lipschitz gradient, it is proved that the orbits converge weakly to a constrained minimizer whenever it exists. This result remains valid even if the initial condition is chosen out of the feasible set and it can be extended in some sense to quasiconvex functions. An asymptotic control result, involving a Tykhonov-like regularization, shows that the orbits can be forced to converge strongly toward a well-specified minimizer. In the finite-dimensional framework, we study the differential inclusion obtained by replacing the classical gradient by the subdifferential of a continuous convex function. We prove the existence of a solution whose asymptotic properties are the same as in the smooth case.
Similar content being viewed by others
References
BrÉzis, H., Opérateurs Maximaux Monotones, North-Holland, Amsterdam, Holland, 1973.
Bruck, R.E., Asymptotic Convergence of Nonlinear Contraction Semigroups in Hilbert Space, Journal of Functional Analysis, Vol. 18, pp. 15-26, 1974.
Polyak, B.T., Introduction to Optimization, Optimization Software, New York, NY, 1987.
Maccormick, G. P, and Tapia, R.A, The Gradient Projection Method under Mild Differentiability Conditions, SIAM Journal on Control and Optimization, Vol. 10, pp. 93-98, 1972.
Martinet, B., Perturbation des Méthodes d'Optimisation: Applications, RAIRO Analyse Numérique, Vol. 12, pp. 153-171, 1978.
Phelps, R.R., The Gradient Projection Method Using Curry's Steplength, SIAM Journal on Control and Optimization, Vol. 24, pp. 692-699, 1986.
Alber, Y. I., Iusem, A. N., and Solodov, M.V., On the Projected Subgradient Method for Nonsmooth Convex Optimization in a Hilbert Space, Mathematical Programming, Vol. 81, pp. 23-25, 1998.
Antipin, A. S., Minimization of Convex Functions on Convex Sets by Means of Differential Equations, Differential Equations, Vol. 30, pp. 1365-1375, 1994.
Attouch, H., and Alvarez, F., The Heavy Ball with Friction Dynamical System for Convex Constrained Minimization Problems, Optimization (Namur, 1998); Attouch, H., and Alvarez, F., Lecture Notes in Economic and Mathematical Systems, Springer, Berlin, Germany, Vol. 481, pp. 23-35, 2000.
Baillon, J.B., Un Exemple Concernant le Comportement Asymptotique de la Solution du Problème du/dt + ∂ϕ(u)∋0, Journal of Functional Analysis, Vol. 28, pp. 369-376, 1978.
Opial, Z., Weak Convergence of the Sequence of Successive Approximations for Nonexpansive Mappings, Bulletin of the American Mathematical Society, Vol. 73, pp. 591-597, 1967.
Attouch, H., and Cominetti, R., A Dynamical Approach to Convex Minimization Coupling Approximation with the Steepest Descent Method, Journal of Differential Equations, Vol. 128, pp. 519-540, 1996.
Attouch, H., and Czarnecki, M.O., Asymptotic Control and Stabilization of Nonlinear Oscillators with Nonisolated Equilibria, Journal of Differential Equations (to appear).
Aubin, J. P., and Cellina, A., Differential Inclusions, Springer Verlag, New York, NY, 1984.
Schatzman, M., A Class of Nonlinear Differential Equations of Second-Order in Time, Nonlinear Analysis, Vol. 2, pp. 355-373, 1978.
Lemaire, B., An Asymptotical Variational Principle Associated with the Steepest Descent Method for a Convex Function, Journal of Convex Analysis, Vol. 3, pp. 63-70, 1996.
Alvarez, F., On the Minimizing Property of a Second-Order Dissipative System in Hilbert Space, SIAM Journal on Control and Optimization, Vol. 38, pp. 1102-1119, 2000.
Goudou, X., The Heavy Ball with Friction System for a Smooth Quasiconvex Function, Working Paper, Université Montpellier II, Montpellier, France.
Kiwiel, K. C., and Murty, K., Convergence of the Steepest Descent Method for Minimizing Quasiconvex Functions, Journal of Optimization Theory and Applications, Vol. 89, pp. 221-226, 1996.
Colli, P., and Visintin, A., On a Class of Doubly Nonlinear Evolution Problems, Communications in Partial Differential Equations, Vol. 15, pp. 737-756, 1990.
Rockafellar, R. T., and Wets, R., Variational Analysis, Springer, New York, NY, 1998.
Rockafellar, R.T., Convex Analysis, Princeton University Press, Princeton, New Jersey, 1970.
Censor, Y., Eggermont, P. P. B., and Gordon, D., Strong Underrelaxation in Kaczmarz's Method for Inconsistent Systems, Numerische Mathematik, Vol. 41, pp. 83-92, 1983.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Bolte, J. Continuous Gradient Projection Method in Hilbert Spaces. Journal of Optimization Theory and Applications 119, 235–259 (2003). https://doi.org/10.1023/B:JOTA.0000005445.21095.02
Issue Date:
DOI: https://doi.org/10.1023/B:JOTA.0000005445.21095.02