Skip to main content
SpringerLink
Log in

Trilinear Monomials with Mixed Sign Domains: Facets of the Convex and Concave Envelopes

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

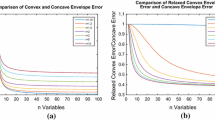
Convex underestimators of nonconvex functions, frequently used in deterministic global optimization algorithms, strongly influence their rate of convergence and computational efficiency. A good convex underestimator is as tight as possible and introduces a minimal number of new variables and constraints. Multilinear monomials over a coordinate aligned hyper-rectangular domain are known to have polyhedral convex envelopes which may be represented by a finite number of facet inducing inequalities. This paper describes explicit expressions defining the facets of the convex and concave envelopes of trilinear monomials over a box domain with bounds of opposite signs for at least one variable. It is shown that the previously used approximations based on the recursive use of the bilinear construction rarely yield the convex envelope itself.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Adjiman, C.S., Androulakis, I.P. and Floudas, C.A. (1998b), A global optimization method, α BB, for general twice differentiable NLPs. I. Implementation and computional results, Computers and Chemical Engineering 22, 1159-1179.

    Google Scholar 

  2. Adjiman, C.S., S. Dallwig, C.A. Floudas, and A. Neumaier (1998a), A global optimization method, αBB, for general twice differentiable NLPs. I. Theoretical advances, Computers and Chemical Engineering 22, 1137-1158.

    Google Scholar 

  3. Al-Khayyal, F.A. and J.E. Falk (1983), Jointly constrained biconvex programming. Mathematics Operation Research 8, 273.

    Google Scholar 

  4. Androulakis, I.P., C.D. Maranas, and C.A. Floudas (1995), αBB: a global optimization method for general constrained nonconvex problems. Journal. of Global Optimization 7, 337-363.

    Google Scholar 

  5. Balas, E. and J. Mazzola (1984), Nonlinear 0–1 Programming: I Linearization techniques. Mathematical Programming 30, 1-21.

    Google Scholar 

  6. Crama, Y. (1989), Recognition problems for special classes of polynomials in 0–1 variables. Mathematical Programming 44, 139-155.

    Google Scholar 

  7. Crama, Y. (1993), Concave extensions for nonlinear 0–1 maximization problems. Mathematical Programming 61, 53-60.

    Google Scholar 

  8. Floudas, C.A. (2000), Deterministic Global Optimization: Theory, Algorithms and Applications. Kluwer Academic Publishers.

  9. Floudas, C.A., A. Aggarwal and A.R. Ciric 1989, Global Optimum Search for Nonconvex NLP and MINLP Problems. Computers and Chemical Engineering 13, 1117-1132.

    Google Scholar 

  10. Glover, F. and E. Woolsey (1974), Converting the 0–1 polynomial programming problem to a linear 0–1 program. Operations Research 22, 180-182.

    Google Scholar 

  11. Hamed, A. S.E. (1991), Calculation of Bounds on Variables and Underestimating Convex Functions for Nonconvex Functions, Ph.D. thesis, George Washington University.

  12. Hammer, P., P. Hansen and B. Simeone (1984), Roof duality, complementation and persistency in quadratic 0–1 optimization. Mathematical Programming 28, 121-155.

    Google Scholar 

  13. Hammer, P. and S. Rudeanu (1968), Boolean Methods in Operations Research and Related Areas. Springer.

  14. Hansen, P. and B. Simeone (1990), On the equivalence of paved duality and standard linearization in nonlinear 0–1 optimization. Discrete Applied Mathematics 29, 187-193.

    Google Scholar 

  15. Maranas, C.D. and C.A. Floudas (1995), Finding all Solutions of Nonlinearly Constrained Systems of Equations, Journal. of Global Optimization. 7, 143-182.

    Google Scholar 

  16. McCormick, G.P. (1976), Computation of Global Solutions to Factorable Nonconvex Programs: Part I-Convex Underestimation Problems. Mathematical Programming 10, 147.

    Google Scholar 

  17. Meyer, C.A. and C.A. Floudas (2003), Trilinear Monomials with Positive or Negative Domains: Facets of the Convex and Concave Envelopes, to appear in Frontiers in Global Optimization, C.A. Floudas and P.M. Pardolos (eds.), Kluwer Academic Publishers.

  18. Rikun, A.D. (1997), A Convex Envelope Formula for Multilinear Functions. Journal. of Global Optimization. 10, 425-437.

    Google Scholar 

  19. Rockafellar, R.T. (1970), Convex Analysis. Princeton University Press.

  20. Ryoo, H.S. and N.V. Sahinidis (2001), Analysis of Bounds for Multilinear Functions. Journal of Global Optimization 19, 403-424.

    Google Scholar 

  21. Sherali, H.D. 1997, Convex Envelopes of Multilinear Functions over a Unit Hypercube and over Special Discrete Sets. Acta Mathematica Vietnamica 22, 245-270.

    Google Scholar 

  22. Sherali, H.D. and C.H. Tuncbilek (1992), A Global Optimization Algorithm for Polynomial Programming Problems Using a Reformulation-Linearization Technique. Jornal. of Global Optimization. 2, 101-112.

    Google Scholar 

  23. Tawarmalani, M. and N.V. Sahinidis (2002), Convex extensions and envelopes of lower semi-continuous functions. Mathematical. Programming Ser. A 1.

Download references

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, Princeton University, Princeton, NJ, 08544, USA

    Clifford A. Meyer & Christodoulos A. Floudas

Authors
  1. Clifford A. Meyer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Christodoulos A. Floudas
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Meyer, C.A., Floudas, C.A. Trilinear Monomials with Mixed Sign Domains: Facets of the Convex and Concave Envelopes. Journal of Global Optimization 29, 125–155 (2004). https://doi.org/10.1023/B:JOGO.0000042112.72379.e6

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/B:JOGO.0000042112.72379.e6

Search

Navigation