Fracture analysis of materials with periodic microstructure by the representative cell method

Abstract

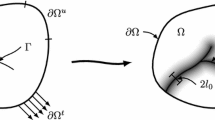
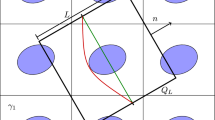
The periodic structure of some natural and especially man-made materials can be manifested not only on an atomic but also on a larger scale. Investigation of mechanical properties of these materials usually hinges on well-developed homogenization methods. On the other hand, these methods are not suitable for fracture analysis where the knowledge of the local stress-strain fields near a flaw (a crack) is required. The result is obtained by the use of the representative cell method based on the discrete Fourier transform. This method enables one to determine the exact stress distribution in a periodic structure subjected to arbitrary loading. Direct application of the method is impossible since the crack violates the translational symmetry defined by the material microstructure. This obstacle is overcome by application of the fictitious loading to the uncracked body at the line where the crack is to be located. The amplitude of the loading is adjusted in order to fulfill the boundary conditions imposed on the crack faces. The compatibility equation for deriving this amplitude is obtained by the use of the corresponding Green function, which is found in a closed form. Fracture problems for the two types of materials with a periodic microstructure are considered. The first one is a composite material consisting of dissimilar isotropic elastic layers arranged periodically. The second periodic microstructure is a 2D infinite beam lattice modeling a cellular material. The analysis of the failure process in the latter case shows that in contrast to the case of homogeneous material, the crack propagation path is not defined by the condition of zero Mode II stress intensity factor.