Plane strain crack problems for elastic materials with variable properties

Abstract

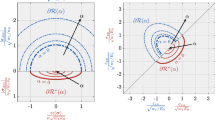
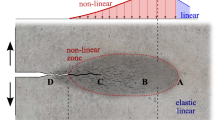
Distributions of stress, strain and displacement occurring at the tip of a crack in a material with properties dependent on the type of loading are investigated for the conditions of plane strain in both far-field tensile and shear loads. The causes of the dependence of material properties on the type of external forces are the various inhomogeneities such as microcracks, pores, inclusions or reinforcing components in a material. The behaviour of these inhomogeneities depends substantially on the conditions of loading or deformation. Hence, the deformation properties of a material are not fixed intrinsic material characteristics that are invariant to the loading conditions, but rather the macroproperties of such materials are stress-state-dependent ones, and this effect becomes more noticeable as the volume content of the inhomogeneities increases. The asymptotic solutions of crack problems are obtained on the basis of proposed stress-strain relations describing not only the stress-state dependence of material properties, but the interrelation between the characteristics of volume and shear deformation as well. In a non-uniform stress state the primary macrohomogeneous material becomes an heterogeneous one. The use of the stress function is not effective for the solution of plane strain crack problems for the materials under consideration. Therefore, an approach based on the corresponding representation for the strains is used. It is shown that the commonly used suppositions of the symmetry or anti-symmetry in the stress distribution relative to the crack plane can not be accepted, since they do not allow all the boundary conditions to be satisfied. The opening of the crack surfaces in the case of far shear field is observed. The influence of stress-state sensitivity of material properties on the values of the stress intensity factor is more significant for tensile crack than for the crack in far shear field.