Abstract
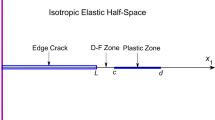
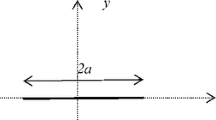
Resistance to dislocation glide in slip bands due to the presence of other dislocations may be represented by an additional term in the integral equation formulation of the equilibrium state. As a consequence, the asymptotic behaviour of dislocation density at the edge of interval is modified from the conventional square root singularity. We propose an efficient and fast numerical method that is suitable for solving the resulting singular equations of the second kind based on the Gauss-Jacobi quadrature. The quadrature formulae involve fixed nodal points and provide exact results for polynomials up to degree 2n-1, where n is the number of nodes. A numerical example of the application of the Gauss-Jacobi rule to a slip band problem is provided as a demonstration of the validity of the method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Atkinson, K.E. (1976) A survey of numerical methods for the solution of Fredholm integral equations of the second kind, SIAM, Philadelphia, PA.
Bilby B.A., and Swinden K.H. (1965) The spread of plastic yield from a notch, Proceedings of the Royal Society of London, A285, 22–32.
Deleves, L.M. and Mohamed, J.L. (1985) Computational methods for integral equations, New York.
Erdogan, F., Gupta, G.D. and Cook, T.S. (1973) Numerical solution of singular integral equation. In Methods of analysis and solutions of crack problems (ed. G. C. Sih). 368–425, Groningen: Noordhoff.
Gerasoulis, A. (1982) The use of piecewise quadratic polynomial for the solution of singular integral equation of Cauchy type, Computers and Mathematics with Applications 8. 15–22
Golberg, M.A. (1984) The convergence of a collocation method for a class of a Cauchy singular integral equations, Journal of Mathematical Analysis and Applications. 100, 500–512.
Groma, I., Csikor, F.F., and Zaiser, M. (2003) Spatial correlations and higher-order gradient terms in a continuum description of dislocation dynamics, Acta Materialia 51, 1271–1281.
Nowell, D. and Hills, D.A. (1987) Open cracks at or near free edges. Journal of Strain Analysis 22, 177–85.
Korsunsky, A.M., and Evans, J.T. (2000) Analysis of cohesive zones in cracks and slip bands using hypersingular interpolative quadratures, International Journal of Fracture, 104, L37–L42.
Miller, G.R., and Keer, L.M., (1985) A numerical technique for solution of singular integral equations of the second kind, Quarterly of Appied Mmathematics. 455–466.
Muskhelishvili, N.I. (1953) Singular integral equations, Noordhoff, Groningen.
Muskhelishvili, N.I. (1949) Some basic problems of mathematical theory of elasticity, Moscow.
Stroud, A. H. and Secrest, D. (1966) Gaussian quadrature formulas. New York: Macmillan.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lifeng, M., Korsunsky, A.M. Effect of Friction on Edge Singularities in Slip Bands. International Journal of Fracture 123, L143–L150 (2003). https://doi.org/10.1023/B:FRAC.0000005807.95505.80
Issue Date:
DOI: https://doi.org/10.1023/B:FRAC.0000005807.95505.80