A Comparison of the Response of Isotropic Inhomogeneous Elastic Cylindrical and Spherical Shells and Their Homogenized Counterparts

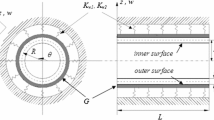
Abstract

All real bodies are inhomogeneous, though in many such bodies the inhomogeneity is “mild” in that the response of the bodies can be “approximated” well by the response of a homogeneous approximation. In this study we explore the status of such approximations when one is concerned with bodies whose response is nonlinear. We find that significant departures in response can occur between that of a “mildly” inhomogeneous body and its homogeneous approximation (if the approximate model is restricted to a certain class), both quantitatively and qualitatively. We illustrate this fact within the context of a specific boundary value problem, the inflation of an inhomogeneous spherical shell. We also discuss the inappropriateness of homogenization procedures that lead to a homogenized stored energy for the body when in fact what is required is a homogenized model that predicts the appropriate stresses as they invariably determine the failure or integrity of the body.