Abstract
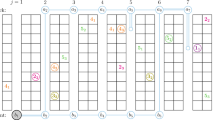
The Sequential Ordering Problem (herewith, SOP) with precedence relationships was introduced in Escudero (1988), and extended to cover release and due dates in Escudero and Sciomachen (1993). It has a broad range of applications, mainly in production planning for manufacturing systems. The problem consists of finding a minimum weight Hamiltonian path on a directed graph with weights on the nodes and the arcs, satisfying precedence relationships among the nodes and given lower and upper bounds on the weights of the Hamiltonian subpaths. In this paper we present a model for the constrained minimum weight Hamiltonian path problem with precedences and due dates forcing constraints, and introduce related valid cuts that can be used in a separation framework for the dual (Lagrangian based) relaxation of the problem. We also provide an heuristic separation procedure to obtain those cuts, so-called the Lagrangian Relax-and-Cut (LRC) scheme. Computational experience is given for variations of some SOP cases already reported in the literature.
Similar content being viewed by others
References
Ascheuer, N. (1995). “Hamiltonian Path Problems in the On-line Optimization of Flexible Manufacturing Systems.” Ph.D. Thesis, Technical University, Berlin, Germany.
Ascheuer, N., L.F. Escudero, M. Grötschel, and M. Stoer. (1993). “A Cutting Plane Approach to the Sequential Ordering Problem (with Applications to Job Scheduling in Manufacturing).” SIAM Journal on Optimization 3, 25–42.
Ascheuer, N., M. Fischetti, and M. Grötschel. (2001). “Solving the Asymmetric Travelling Salesman Problem with Time Windows by Branch & Cut.” Mathematical Programming 90, 475–506.
Ascheuer, N., M. Jünger, and G. Reinelt. (2000). “A Branch & Cut Algorithm for the Asymmetric Hamiltonian Path Problem with Precedence Constraints.” Computational Optimization and Applications 17, 61–84.
Balas, E., M. Fischetti, and W.R. Pulleyblank. (1995). “The Precedence-Constrained Asymmetric Traveling Salesman Polytope.” Mathematical Programming 68, 241–265.
Balas, E. and N. Simonetti. (2001). “Linear Time Dynamic-Programming Algorithms for New Classes of Restricted TSPs: A Computational Study.” INFORMS Journal on Computing 13, 56–75.
Dumas, Y., J. Desrosiers, and E. Gelinas. (1995). “An Optimal Algorithm for the Traveling Salesman Problem with Time Windows.” Operations Research 43, 367–371.
Edmonds, J. (1967). “Optimum Branchings.” Journal of Research of the National Bureau of Standards B 71, 233–240.
Escudero, L.F. (1988). “An Inexact Algorithm for the Sequential Ordering Problem.” European Journal of Operational Research 37, 236–253.
Escudero, L.F., A. Garín, and G. Pérez. (1994). “On Improving the Dietrich-Escudero Approach for Tightening Cover Induced Inequalities.” European Journal of Operational Research 73, 167–168.
Escudero, L.F., M. Guignard, and K. Malik. (1994). “A Lagrangian Relax-and-Cut Approach for the Sequential Ordering Problem with Precedence Relationships.” Annals of Operations Research 50, 219–237.
Escudero, L.F. and A. Sciomachen. (1993). “Local Search Procedures for Improving Feasible Solutions to the Sequential Ordering Problem.” Annals of Operations Research 43, 397–416.
Escudero, L.F. and A. Sciomachen. (1999). “A O(n3) Algorithm for Finding a Feasible Solution for the Sequential Ordering Problem.” Journal of Combinatorics, Information and System Sciences 24, 1–23.
Fischetti, M. and P. Toth. (1993). “An Efficient Algorithm for the Min-Sum Arborescence Problem on Complete Digraphs.” ORSA Journal on Computing 5, 426–434.
Gambardella, L.M. and M. Dorigo. (1997). “HAS-SOP: Hybrid Ant System for the Sequential Ordering Problem.” Technical Report IDSIA-11-97, IDSIA, Lugano, Switzerland.
Gambardella, L.M. and M. Dorigo. (2000). “An Ant Colony System Hybridized with a New Local Search for the Sequential Ordering Problem.” INFORMS Journal on Computing 12, 237–255.
Geoffrion, A. (1974). “Lagrangian Relaxation and Its Uses in Integer Programming.” Mathematical Programming Study 2, 82–114.
Held, M. and R.M. Karp. (1970). “The Traveling Salesman Problem and Minimum Spanning Trees.” Operations Research 18, 1138–1162.
Held, M. and R.M. Karp. (1971). “The Traveling Salesman Problem and Minimum Spanning Trees: Part II,“ Mathematical Programming 1, 62–88.
Hoogeveen, J.A. and S.L. van de Velde. (1995). “Stronger Lagrangian Bounds by the Use of Slack Variables with Applications to Machine Scheduling Problems.” Mathematical Programming 70, 173–190.
Moon, C., J. Kim, G. Choi, and Y. Seo. (2002). “An Efficient Genetic Algorithm for the Traveling Salesman Problem with Precedence Constraints.” European Journal of Operational Research 140, 606–617.
Ortuño, M.T. (1995). “Sobre Cortes Lagrangianos Fuertes en la Resolución del Problema del Ordenamiento Secuencial.” Ph.D. Thesis, Universidad Complutense de Madrid, Spain.
Potts, C.N. (1985). “A Lagrangian Based Branch-and-Bound Algorithm for Single Machine Sequencing with Precedence Constraints to Minimize Total Weighted Completion Time.” Management Science 31, 1300–1311.
Salomon, M.M. (1995). “An Optimal Algorithm for the Traveling Salesman Problem with TimeWindows.” Operations Research 43, 367–371.
van de Velde, S.L. (1991). “Machine Scheduling and Lagrangian Relaxation.” Ph.D. Thesis, CWI, Amsterdam, The Netherlands.
van de Velde, S.L. (1995). “Dual Decomposition of a Single-Machine Scheduling Problem.” Mathematical Programming 69, 413–428.
Wikum, E.D., D.C. Llewellyn, and G.L. Nemhauser. (1994). “One-Machine Generalized Precedence Constrained Scheduling Problems.” Operations Research Letters 16, 87–99.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Alonso-Ayuso, A., Detti, P., Escudero, L.F. et al. On Dual Based Lower Bounds for the Sequential Ordering Problem with Precedences and Due Dates. Annals of Operations Research 124, 111–131 (2003). https://doi.org/10.1023/B:ANOR.0000004765.69773.41
Issue Date:
DOI: https://doi.org/10.1023/B:ANOR.0000004765.69773.41