Exact Connections of Warping Fields and Torsional Rigidities of Symmetric Composite Bars

Abstract

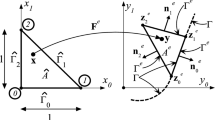
Saint-Venant's torsion of symmetric cylindrical bars consisting of two or four homogeneous phases is studied. A symmetric section is meant that the cross section of the cylindrical bar possesses reflectional symmetry with respect to one or more axes. Each constituent region may have different shear modulus. The idea of the analysis is to superimpose suitably reflected potentials to obtain the torsion solution of the same composite section but with different moduli. For two-phase sections, we show that, if the warping fields for a given symmetric section with phase shear moduli μ₁ and μ₂ are known a priori, then the warping fields for the same configuration but with a different set of constituent moduli μ₁ ^′ and μ₂ ^′ are readily found through simple linear superpositions. Further, suppose that the torsional rigidities T(μ₁,μ₂) and T(μ₁ ^′,μ₂ ^′) for any two sets of phase moduli can be measured by some experimental tests or evaluated through numerical procedures, then the torsional rigidity for any other combinations of constituent moduli T(μ₁ ^′′,μ₂ ^′′) can be exactly determined without any recourse to the field solutions of governing differential equations. Similar procedures can be applied to a 4-phase symmetric section. But the coefficients of superposition are only found for a few branches. Specifically, we find that depending on the conditions of μ and μ^′, admissible solutions can be divided into three categories. When the correspondence between the warping field is known to exist, a link between the torsional rigidities can be established as well.