Abstract
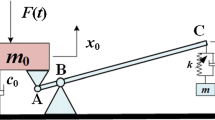
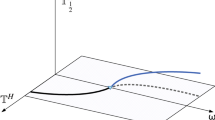
We consider the problem of 1:1 resonance in autonomous, timereversible systems. We first present an abstract treatment for n-dimensionalsecond-order systems, and then apply our method to two simplemechanical examples involving follower loads. As the magnitude of the follower load is increased past a criticalvalue, the trivial solution loses stability as the real-valuedfrequencies of the linearized system first coalesce and then splitapart with complex-conjugate values. In Hamiltonian systems this isusually referred to as the Hamiltonian–Hopf bifurcation. Some novelfeatures of our analysis are the direct exploitation of reversibilityand a Liapunov–Schmidt reduction of the second-order (Newtonian)equations of motion, the latter of which requires no complexification.The analysis of the resulting two-parameter, one-dimensionalbifurcation equation yields the possibility that families ofnontrivial periodic solutions may exist for load values in excess of the critical value.
Similar content being viewed by others
References
Vanderbauwhede, A., 'Hopf bifurcation for equivariant conservative and time-reversible systems', Proceedings of the Royal Society of Edinburgh. Section A. Mathematics 116(1–2), 1990, 103–128.
Golubitsky, M., Marsden, J. E., Stewart, I., and Dellnitz, M., 'The constrained Liapunov–Schmidt procedure and periodic orbits', in Normal Forms and Homoclinic Chaos Waterloo, ON, 1992, American Mathematical Society, Providence, RI, 1995, pp. 81–127.
O'Reilly, O. M., Malhotra, N. K., and Namachchivaya, N. S., 'Some aspects of destabilization in reversible dynamical systems with application to follower forces', Nonlinear Dynamics 10(1), 1996, 63–87.
Timoshenko, S. P., Theory of Elastic Stability, McGraw-Hill, New York, 1961.
Ziegler, H., Principles of Structural Stability, Blaisdell, Waltham, MA, 1968.
Herrmann, G. and Bungay, R. W., 'On the stability of elastic systems subjected to nonconservative forces', ASME, Journal of Applied Mechanics 31, 1964, 435–440.
Jin, J.-D. and Matsuzaki, Y., 'Bifurcations in a two-degree-of-freedom elastic system with follower forces', Journal of Sound and Vibration 126(2), 1988, 265–277.
Thomsen, J. J., 'Chaotic dynamics of the partially follower-loaded elastic double pendulum', Journal of Sound and Vibration 188(3), 1995, 385–405.
Herrmann, G. and Jong, I. C., 'On nonconservative stability problems of elastic systems with slight damping', ASME, Journal of Applied Mechanics 33, 1966, 125–133.
Joseph, P., Pandiyan, R., and Sinha, S. C., 'Optimal control of mechanical systems subjected to periodic loading via Chebyshev polynomials', Optimal Control Applications and Methods 14(2), 1993, 75–90.
Joseph, P. and Sinha, S. C., 'Control of general dynamic systems with periodically varying parameters via Liapunov–Floquet transformation', ASME, Journal of Dynamic Systems, Measurement, and Control 116, 1994, 650–658.
Golubitsky, M. and Schaeffer, D. G., Singularities and Groups in Bifurcation Theory. Vol. I, Springer, New York, 1985.
Crandall, M. and Rabinowitz, P., 'Bifurcation from simple eigenvalues', Journal of Functional Analysis 8, 1971, 321–340.
Golubitsky, M., Stewart, I., and Schaeffer, D. G., Singularities and Groups in Bifurcation Theory. Vol. II, Springer, New York, 1988.
Antman, S. S., Nonlinear Problems of Elasticity, Springer, New York, 1995.
Bolotin, V. V., Nonconservative Problems of the Theory of Elastic Stability, Macmillan, New York, 1963.
Healey, T. J. and Kielhöfer, H., 'Free nonlinear vibrations for a class of two-dimensional plate equations: Standing and discrete-rotating waves', Nonlinear Analysis 29(5), 1997, 501–531.
Kato, T., Perturbation Theory for Linear Operators, Springer, New York, 1966.
Kielhöfer, H., 'Bifurcation of periodic solutions for a semilinear wave equation', Journal of Mathematical Analysis and Applications 68(2), 1979, 408–420.
Leipholz, H., Stability Theory. An Introduction to the Stability of Dynamic Systems and Rigid Bodies, Academic Press, New York, 1970 [Translated from German by Scientific Translation Service].
Leipholz, H., Stability of Elastic Systems, Sijthoff & Noordhoff, Alphen aan den Rijn, 1980 [translated from German].
MacEwen, K.W., 'Large amplitude oscillations of elastic rods', Ph.D. Thesis, Cornell University, NY, 1999.
Vanderbauwhede, A., 'Hopf bifurcation at nonsemisimple eigenvalues', in Multiparameter Bifurcation Theory, Arcata, CA, 1985, American Mathematical Society, Providence, RI, 1986, pp. 343–353.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
MacEwen, K.W., Healey, T.J. A Simple Approach to the 1:1 Resonance Bifurcation in Follower-Load Problems. Nonlinear Dynamics 32, 143–159 (2003). https://doi.org/10.1023/A:1024434731623
Issue Date:
DOI: https://doi.org/10.1023/A:1024434731623