Abstract
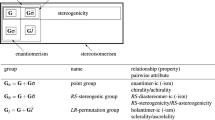
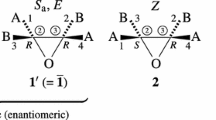
Molecules of ligancy 4 that have been derived from an allene, an ethylene, a tetrahedral, and a square-planar skeleton have been investigated to show that their symmetries are dually and distinctly controlled by point groups and permutation groups. Insomuch as the point-group symmetry was exhibited to control the chirality/achirality of a molecule, sphericity in a molecule, and enantiomeric relationship between molecules [S. Fujita, J. Am. Chem. Soc. 112 (1990) 3390], the permutation-group symmetry has been now clarified to control the stereogenicity of a molecule, tropicity in a molecule, and diastereomeric relationship between molecules. To characterize permutation groups, proper and improper permutations have been defined by comparing proper and improper rotations. Thereby, such permutation groups are classified into stereogenic and astereogenic ones. After a coset representation (CR) of a permutation group has been ascribed to an orbit (equivalence class), the tropicity of the orbit has been defined in term of the global stereogenicity and the local stereogenicity of the CR. As a result, the conventional “stereogenicity” has now been replaced by the concept local stereogenicity of the present investigation. The terms homotropic, enantiotropic, and hemitropic are coined and used to characterize prostereogenicity. Thus, a molecule is defined as being prostereogenic if it has at least one enantiotropic orbit. Since this definition has been found to be parallel with the definition of prochirality, relevant concepts have been discussed with respect to the parallelism between stereogenicity and chirality in order to restructure the theoretical foundation of stereochemistry and stereoisomerism. The derivation of the skeletons has been characterized by desymmetrization due to the subduction of CRs. The Cahn–Ingold–Prelog (CIP) system has been discussed from the permutational point of view to show that it specifies diastereomeric relationships only. The apparent specification of enantiomeric relationships by the CIP system has been shown to stem from the fact that diastereomeric relationships and enantiomeric ones overlap occasionally in case of tetrahedral molecules.
Similar content being viewed by others
References
E. Eliel and S.H. Wilen, Stereochemisty of Organic Compounds (Wiley, New York, 1994).
S.R. Buxton and S.M. Roberts, Guide to Organic Stereochemisty (Addison-Wesley, Longman, New York, 1996).
A. von Zelewsky, Stereochemisty of Coordination Compounds (Wiley, Chichester, 1996).
J.H. van't Hoff, Archives Néerlandaises des Sciences exactes et naturelles 9 (1874) 445–454.
A.M. Rouhi, Chem. Engrg. News (September 6) (1999) 28–32.
J.K. O'Loane, Chem. Rev. 80 (1980) 41–61.
E.L. Eliel, J. Chem. Educ. 57 (1980) 52–55.
R.S. Cahn, C.K. Ingold and V. Prelog, Angew. Chem. Int. Ed. Engl. 5 (1966) 385.
K.R. Hanson, J. Am. Chem. Soc. 88 (1966) 2731–2472.
K. Mislow and J. Siegel, J. Am. Chem. Soc. 106 (1984) 3319–3328.
G.E. McCasland, A New General System for the Naming of Stereoisomers (Chemical Abstracts, Columbus, 1953).
V. Prelog and G. Helmchen, Angew. Chem. Int. Ed. Engl. 21 (1982) 567–583.
P. Mata, A.M. Lobo, C. Marshall and A.P. Johnson, Tetrahedron: Asymmetry 4 (1993) 657–668.
M. Perdih and M. Razinger, Tetrahedron: Asymmetry 5 (1994) 835–861.
P. Mata and R.B. Nachbar, Tetrahedron: Asymmetry 6 (1995) 693–696.
S. Fujita, J. Am. Chem. Soc. 112 (1990) 3390–3397.
S. Fujita, Theor. Chim. Acta 76 (1989) 247–268.
S. Fujita, Symmetry and Combinatorial Enumeration in Chemistry (Springer-Verlag, Berlin, Heidelberg, 1991).
S. Fujita, Tetrahedron 46 (1990) 5943–5954.
K. Mislow and M. Raban, Top. Stereochem. 1 (1967) 1–38.
S. Fujita, Bull. Chem. Soc. Jpn. 64 (1991) 439–449.
S. Fujita, J. Math. Chem. 5 (1990) 121–156.
S. Fujita, Bull. Chem. Soc. Jpn. 63 (1990) 203–215.
S. Fujita, Tetrahedron 46 (1990) 365–382.
S. Fujita, Bull. Chem. Soc. Jpn. 72 (1999) 13–20.
S. Fujita, J. Chem. Inf. Comput. Sci. 39 (1999) 151–163.
F. Harary and E.M. Palmer, Graphical Enumeration (Academic Press, New York, 1973).
A.T. Balaban (ed.), Chemical Applications of Graph Theory (Academic Press, London, 1976).
G. Pólya and R.C. Read, Combinatorial Enumeration of Groups, Graphs, and Chemical Compounds (Springer-Verlag, New York, 1987).
S. Fujita, Bull. Chem. Soc. Jpn. 74 (2001) 1585–1603.
S. Fujita, Tetrahedron 47 (1991) 31–46.
K.A. Black, J. Chem. Educ. 67 (1990) 141–142.
V. Prelog and G. Helmchen, Helv. Chim. Acta 55 (1972) 2581.
V. Prelog, Science 193 (1976) 17–24.
I. Ugi, J. Bungundji, R. Kopp and D. Marquarding, Perspectives in Theoretical Stereochemistry, Lecture Notes in Chemistry, Vol. 36 (Springer-Verlag, Heidelbelg, 1984).
I. Ugi, Chimia 40 (1986) 340–350.
J.G. Nourse, J. Am. Chem. Soc. 101 (1979) 1210–1216.
E. Ruch, Acc. Chem. Res. 5 (1972) 49–56.
J. Hinze (ed.), The Permutation Group in Physics and Chemistry, Lecture Notes in Chemistry, Vol. 12 (Springer-Verlag, Berlin, Heidelberg, 1979).
J. Brocas, M. Gielen and R. Willem, The Permutational Approach to Dynamic Stereochemistry (McGraw-Hill, New York, 1983).
I. Ugi, D. Marquading, H. Klusacek, G. Gokel and P. Gillespie, Angew. Chem. Int. Ed. 9 (1970) 703.
C.A. Mead, Symmetry and Chirality, Topics in Current Chemistry, Vol. 49 (Springer-Verlag, Berlin, Heidelbelg, New York, 1974).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Fujita, S. Stereogenicity/Astereogenicity as Global/Local Permutation-Group Symmetry and Relevant Concepts for Restructuring Stereochemistry. Journal of Mathematical Chemistry 33, 113–143 (2003). https://doi.org/10.1023/A:1023251932146
Issue Date:
DOI: https://doi.org/10.1023/A:1023251932146