Abstract
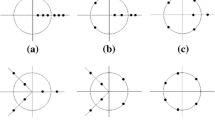
The families of periodic solutions to an autonomous Hamiltonian system in that part where the solutions are unstable have their specific “field of influence.” Under strong instability, the orbits that have fallen in such a “field of influence” are drawn into the family as in a whirlpool and then are thrown away from it. In the particular case of the restricted three-body problem, the orbits around the libration points L 1 and L 2 are super-unstable and the Keplerian elements in motion over these orbits change drastically. When the orbits fall into such a domain, for some time the motion is close to the motion around the libration point, and after being thrown out of this domain, the Keplerian orbital elements also change essentially.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
Egorov, V.A. and Gusev, L.I., Dinamika pereletov mezhdu Zemlei i Lunoi (Dynamics of Flights between the Earth and the Moon), Moscow: Nauka, 1980.
Poincare, H., Les Methodes Nouvelles de la Mecanique Celeste, vols. 1–3, Paris: Gauthier-Villars, 1892. Translated in Russian as Puankare, A., Selected Papers, vols. 1–2, Moscow: Nauka, 1971.
Bruno, A.D., Ogranichennaya zadacha trekh tel (Restricted Three-Body Problem), Moscow: Nauka, 1990.
Szebehely, V., Theory of Orbits. The Restricted Problem of Three Bodies, New York and London: Academic, 1967. Translated under the title Teoriya orbit: ogranichennaya zadacha trekh tel, Moscow: Nauka, 1982.
Markeev, A.P., Tochki libratsii v nebesnoi mekhanike i kosmodinamike (Libration Points in Celestial Mechanics and Astrodynamics), Moscow: Nauka, 1978.
Broucke, M.R., Periodic Orbits in the Restricted Three-Body Problem with Earth-Moon Masses, NASA Techn. Rep. 32–1168, Pasadena, 1968.
Bruno, A.D., Nonrecurrent Periodic Solutions to the Restricted Three-Body Problem for the Sun-Jupiter Case, Preprint of Keldysh Inst. of Appl. Math., Rus. Acad. Sci., Moscow, 1993, no. 66.
Kreisman, B.B., Symmetrical Periodic Solutions to the Planar Restricted Three-Body Problem, Preprint of Lebedev Phys. Inst., Rus. Acad. Sci., 1997, no. 66.
Lidov, M.L., Kurs lektsii po teoreticheskoi mekhanike (A Lecture Course in Theoretical Mechanics), Moscow: Fizmatlit, 2001.
Yakubovich, V.A. and Starzhinskii, V.M., Lineinye differentsial'nye uravneniya s periodicheskimi koeffitsientami i ikh prilozheniya (Linear Differential Equations with Periodic Coefficients and Their Applications), Moscow: Nauka, 1972.
Andreyanov, V.V., Kardashev, N.S., Popov, M.V., et al., “Radioastron”: A Radio Interferometer with the Earth-Space Base, Astron. Zh., 1986, vol. 63, no. 5, pp. 850–-855.
Kardashev, N.S., Kreisman, B.B., and Ponomarev, Yu.N., A New Orbit and New Capabilities of the RADIOASTRON Project, in Radioastronomicheskaya tekhnika i metody (Instrumentation and Methods of Radio Astronomy), vol. 228 of Trudy FIAN, Moscow: FIAN, 2000, pp. 3–12.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kreisman, B.B. Gravitation Maneuver Using the Families of Super-Unstable Orbits around the Libration Points. Cosmic Research 41, 51–62 (2003). https://doi.org/10.1023/A:1022303713453
Issue Date:
DOI: https://doi.org/10.1023/A:1022303713453