Skip to main content
SpringerLink
Log in

Modelling of Ground Moling Dynamics by an Impact Oscillator with a Frictional Slider

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

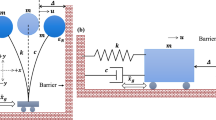
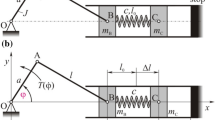
This paper describes current research into the mathematical modelling of a vibro-impact ground moling system. Due to the structural complexity of such systems, in the first instance the dynamic response of an idealised impact oscillator is investigated. The model is comprised of an harmonically excited mass simulating the penetrating part of the mole and a visco-elastic slider, which represents the soil resistance. The model has been mathematically formulated and the equations of motion have been developed. A typical nonlinear dynamic analysis reveals a complex behaviour ranging from periodic to chaotic motion. It was found out that the maximum progression coincides with the end of the periodic regime.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Barkan, D.D., Dynamics of Bases and Foundations, McGraw-Hill, New York, 1962.

    Google Scholar 

  2. Fairweather, N.M., An Investigation of the Driving Mechanism of the Vibrohammer, PhD Thesis, University of Aberdeen, 1984.

  3. Galvanetto, U. and Bishop, S.R., ‘Stick-slip vibrations of a 2-degree-of-freedom geophysical fault model’, Int. J. Mech. Sci. 36 (1994) 683.

    Google Scholar 

  4. Krivtsov, A.M. and Wiercigroch, M., ‘Dry friction model of percussive drilling’, Meccanica 34 (1999) 425.

    Google Scholar 

  5. Krivtsov, A.M. and Wiercigroch, M., ‘Penetration rate prediction for percussive drilling via dry friction model’, Chaos Solitons Fract. 11 (2000) 2479.

    Google Scholar 

  6. Lok, H.P., Neilson, R.D. and Rodger, A.A., ‘Computer-based model of vibro-impact driving’, in: Proceedings of ASME DETC: Symposium on Nonlinear Dynamics in Engineering Systems, Las Vegas, 1999.

  7. Natsiavas, S., ‘Periodic response and stability of oscillators with trilinear restoring force’, J. Sound Vibr. 134 (1989) 315.

    Google Scholar 

  8. Neilson, R.D., Rodger, A.A. and Stevenson, R.G., ‘Development of a computer based model of vibro-impact driving’, Mach. Vibr. 3 (1995) 164.

    Google Scholar 

  9. Pavlovskaia, E., Wiercigroch, M. and Grebogi, C., ‘Modelling of an impact system with a drift’, Phys. Rev. E 64 (2001) 056224.

    Google Scholar 

  10. Pavlyuk, N.P., Bull. Leningrad Struct. Inst. 15 (1931).

  11. Preobrazhenskaya, N.A., ‘Experimental investigations of vibration sinking of piles and channels’, in: Dinamika Gruntov, Gosstroizdat, 27, 1955.

  12. Preobrazhenskaya, N.A. and Savchenko, I.A., ‘On the influence of vibrations on the resistance of clayey soils to shear’, in: Dinamika Gruntov, Gosstroizdat 32, 1958.

  13. Rodger, A.A. and Littlejohn, G.S., ‘A study of vibratory driving in granular soils’, Geotechnique 30 (1980) 269.

    Google Scholar 

  14. Savchenko, I.-A., ‘Influence of vibrations on the internal friction of sands’, in: Dinamika Gruntov, Gosstroizdat, 32, 1958.

  15. Shaw, S.W. and Holmes, P.J., ‘A periodically forced piecewise linear oscillator’, J. Sound Vibr. 90 (1983) 129.

    Google Scholar 

  16. Spektor, M., ‘Principles of soil-tool interaction’, J. Terramech. 18 (1981) 51.

    Google Scholar 

  17. Tsaplin, S., ‘Vibratory impact mechanisms for road and bridge construction’, Autotranzidat, 1953 (translated by the National Engineering Laboratory).

  18. Watanabe, T., ‘Forced vibration of continuous system with nonlinear boundary conditions’, J. Mech. Des. 100 (1978) 487.

    Google Scholar 

  19. Wiercigroch, M., ‘A note on the switch function for the stick-slip phenomenon’, J. Sound Vibr. 175 (1994) 700.

    Google Scholar 

  20. Wiercigroch, M. and Sin, V.T.W., ‘Experimental study of base excited symmetrically piecewise linear oscillator’, ASME J. Appl. Mech. 65(3) (1998) 657.

    Google Scholar 

  21. Wiercigroch, M., Krivtsov, A. and Wojewoda, J., in: Wiercigroch, M. and de Kraker, B. (eds), Nonlinear Dynamics and Chaos of Mechanical Systems with Discontinuities, Chap. 16, World Scientific, Singapore, 2000.

    Google Scholar 

  22. Woo, K.-C., Rodger, A.A., Neilson, R.D. and Wiercigroch, M., ‘Application of the harmonic balance method to ground moling machines operating in periodic regimes’, Chaos, Solitons Fract. 11(15) (2000) 2515.

    Google Scholar 

  23. Yorke, J.A. and Nusse, H.E., Dynamics, Springer, New York, 1998.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centre for Applied Dynamics Research, Department of Engineering, University of Aberdeen, Fraser Noble Bldg. King's College, AB24 3UE, Aberdeen, Scotland, U.K

    Ekaterina Pavlovskaia, Marian Wiercigroch, Ko-Choong Woo & Albert A. Rodger

Authors
  1. Ekaterina Pavlovskaia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marian Wiercigroch
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ko-Choong Woo
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Albert A. Rodger
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pavlovskaia, E., Wiercigroch, M., Woo, KC. et al. Modelling of Ground Moling Dynamics by an Impact Oscillator with a Frictional Slider. Meccanica 38, 85–97 (2003). https://doi.org/10.1023/A:1022023502199

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1022023502199

Search

Navigation