Skip to main content
SpringerLink
Log in

Long-Step Primal Path-Following Algorithm for Monotone Variational Inequality Problems

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

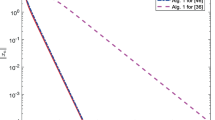
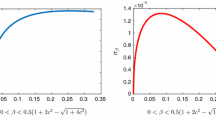
In this paper, we present a long-step primal path-following algorithm and prove its global convergence under usual assumptions. It is seen that the short-step algorithm is a special case of the long-step algorithm for a specific selection of the parameters and the initial solution. Our theoretical result indicates that the long-step algorithm is more flexible. Numerical results indicate that the long-step algorithm converges faster than the short-step algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Rockafellar, R. T., Lagrange Multipliers and Variational Inequalities, Variational Inequalities and Complementarity Problems: Theory and Applications, Edited by R. W. Cottle, F. Giannessi, and J. L. Lions, Wiley, New York, New York, pp. 303–322, 1980.

    Google Scholar 

  2. Pang, J. S., and Chan, D., Iterative Methods for Variational and Complementarity Problems, Mathematical Programming, Vol. 24, pp. 284–313, 1982.

    Google Scholar 

  3. Dafermos, S., Traffic Equilibria and Variational Inequalities, Transportation Science, Vol. 14, pp. 42–54, 1980.

    Google Scholar 

  4. Dafermos, S., An Iterative Scheme for Variational Inequalities, Mathematical Programming, Vol. 26, pp. 40–47, 1983.

    Google Scholar 

  5. Gabay, D., Applications of the Method of Multipliers to Variational Inequalities, Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems, Edited by R. Fortin and R. Glowinski, North-Holland, Amsterdam, Holland, pp. 299–334, 1983.

    Google Scholar 

  6. Tseng, P., Further Applications of a Splitting Algorithm to Decomposition in Variational Inequalities and Convex Programming, Mathematical Programming, Vol. 48, pp. 249–264, 1990.

    Google Scholar 

  7. Marcotte, P., and Wu, J. H., On the Convergence of Projection Methods: Application to the Decomposition of Affine Variational Inequalities, Journal of Optimization Theory and Applications, Vol. 85, pp. 347–362, 1995.

    Google Scholar 

  8. Fukushima, M., Equivalent Differentiable Optimization Problems and Descent Methods for Asymmetric Variational Inequality Problems, Mathematical Programming, Vol. 48, pp. 161–220, 1990.

    Google Scholar 

  9. Taji, K., Fukushima, M., and Ibaraki, T., A Globally Convergent Newton Method for Solving Monotone Variational Inequalities, Mathematical Programming, Vol. 58, pp. 369–383, 1993.

    Google Scholar 

  10. Wu, J. H., Florian, M., and Marcotte, P., A General Descent Framework for Monotone Variational Inequality Problems, Mathematical Programming, Vol. 61, pp. 281–300, 1993.

    Google Scholar 

  11. Harker, P. T., and Pang, J. S., Finite-Dimensional Variational Inequalities and Nonlinear Complementarity Problems: A Survey of Theory, Algorithms and Applications, Mathematical Programming, Vol. 48, pp. 161–220, 1990.

    Google Scholar 

  12. Pang, J. S., Newton's Method for B-Differentiable Equation, Mathematics of Operations Research, Vol. 15, pp. 311–341, 1990.

    Google Scholar 

  13. Pang, J. S., A B-Differentiable Equation Based, Globally and Locally Quadratically Convergent Algorithm for Nonlinear Programs, Complementarity, and Variational Inequality Problems, Mathematical Programming, Vol. 51, pp. 101–131, 1991.

    Google Scholar 

  14. Karmarkar, N., A New Polynomial-Time Algorithm for Linear Programming, Combinatorica, Vol. 4, pp. 373–395, 1984.

    Google Scholar 

  15. Kojima, M., Mizuno, S., and Yoshise, A., A Primal-Dual Interior-Point Algorithm for Linear Programming, Progress in Mathematical Programming: Interior-Point and Related Methods, Edited by N. Megiddo, Springer Verlag, New York, New York, pp 29–47, 1989.

    Google Scholar 

  16. Goldfarb, D., and Liu, S., An O(n 3L) Primal Interior-Point Algorithm for Convex Quadratic Programming, Mathematical Programming Vol. 49, pp. 325–340, 1991.

    Google Scholar 

  17. Sheu, R. L., and Fang, S. C., Insights into the Interior-Point Methods, Report No. 252, Operations Research Program, North Carolina State University, 1990.

  18. Roos, C., and Vial, J. P., Long Step with the Logarithmic Penalty Barrier Function in Linear Programming, Economic Decision-Making: Games, Economics and Optimization, Edited by J. Gabszevwicz, J. F. Richard, and L. Wolsey, Elsevier Science Publishers, Amsterdam, Netherlands, pp. 433–441, 1990.

    Google Scholar 

  19. Kortanek, K. O., Potra, F., and Ye, Y., On Some Efficient Interior-Point Methods for Nonlinear Convex Programming, Linear Algebra and Its Applications, Vol. 152, pp. 169–189, 1991.

    Google Scholar 

  20. Tseng, P., Global Linear Convergence of a Path-Following Algorithm for Some Monotone Variational Inequality Problems, Journal of Optimization Theory and Applications, Vol. 75, pp. 265–279, 1992.

    Google Scholar 

  21. Wu, J. H., Interior-Point Algorithms for Some Monotone Variational Inequality Problems, Publication 879, Centre de Recherche sur les Transports, Université de Montréal, 1993.

  22. Kortanek, K. O., and Zhu, J., A Polynomial Barrier Algorithm for Linearly Constrained Convex Programming Problems, Mathematics of Operations Research, Vol. 1, pp. 116–127, 1993.

    Google Scholar 

  23. Wright, M. H., Interior Methods for Constrained Optimization, Acta Numerica, pp. 341–407, 1992.

  24. Zhu, J., A Path-Following Algorithm for a Class of Convex Programming Problems, Zeitschrift fur Operations Research, Vol. 36, pp. 359–377, 1992.

    Google Scholar 

  25. Ye, Y., and Potra, F., An Interior-Point Algorithm for Solving Entropy Optimization Problems with Globally Linear and Locally Quadratic Convergence Rate, Working Paper, College of Business Administration, University of Iowa, 1990.

  26. Nesterov, Y., and Nemiroskii, A., Interior-Point Polynomial Algorithm in Convex Programming, SIAM, Philadelphia, Pennsylvania, 1994.

    Google Scholar 

  27. Hertog, D., Interior-Point Approach to Linear, Quadratic, and Convex Programming, Kluwer Academic Publishers, Dordrecht, Netherlands, 1994.

    Google Scholar 

  28. Fiacco, A. V., and McCormick, G. P., Nonlinear Programming: Sequential Unconstrained Minimization Techniques, SIAM, Philadelphia, Pennsylvania, 1990.

    Google Scholar 

  29. GÜler, O., Existence of Interior Points and Interior Paths in Nonlinear Monotone Complementarity Problem, Mathematics of Operations Research, Vol. 1, pp. 128–147, 1993.

    Google Scholar 

  30. Bazaraa, M. S., Sherali, H. D., and Shetty, C. M., Nonlinear Programming: Theory and Algorithms, John Wiley and Sons, New York, New York, 1993.

    Google Scholar 

Download references

Author information

Author notes

  1. J. H. Wu (Researcher)

    Present address: INRO Consultants, Montréal, Québec, Canada

Authors and Affiliations

  1. Center for Research on Transportation, Université de Montréal, Montréal, Québec, Canada;

    J. H. Wu (Researcher)

Authors
  1. J. H. Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wu, J.H. Long-Step Primal Path-Following Algorithm for Monotone Variational Inequality Problems. Journal of Optimization Theory and Applications 99, 509–531 (1998). https://doi.org/10.1023/A:1021786630040

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1021786630040

Search

Navigation