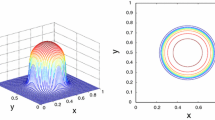
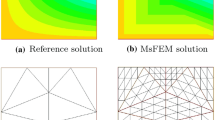
Abstract
We present the results of a study on a posteriori error control strategies for finite volume element approximations of second order elliptic differential equations. Finite volume methods ensure local mass conservation and, combined with some up-wind strategies, give monotone solutions. We adapt the local refinement techniques known from the finite element method to the finite volume discretizations of various boundary value problems for steady-state convection–diffusion–reaction equations. In this paper we derive and study a residual type error estimator and illustrate its practical performance on a series of computational tests in 2 and 3 dimensions. Our tests show that the discussed locally conservative approximation methods with a posteriori error control can be used successfully in numerical simulation of fluid flow and transport in porous media.
Similar content being viewed by others
References
L. Angermann, An a-posteriori estimation for the solution of an elliptic singularly perturbed problem, IMA J. Numer. Anal. 12 (1992) 201-215.
L. Angermann, Balanced a posteriori error estimates for finite-volume type discretizations of convection-dominated elliptic problems, Computing 55(4) (1995) 305-324.
D.N. Arnold, A. Mukherjee and L. Pouly, Locally adapted tetrahedral meshes using bisection, SIAM J. Sci. Comput. 22(2) (2000) 431-448.
I. Babuska and W.C. Rheinboldt, Error estimates for adaptive finite element computations, SIAM J. Numer. Anal. 15 (1978) 736-754.
R.E. Bank and R.K. Smith, A posteriori error estimates based on hierarchical bases, SIAM J. Numer. Anal. 30 (1993) 921-932.
R. Becker, C. Johnson and R. Rannacher, Adaptive error control for multigrid finite element methods, Computing 55(4) (1995) 271-288.
R. Becker and R. Rannacher, A feed-back approach to error control in finite element methods: Basic analysis and examples, East-West J. Numer. Math. 4(4) (1996) 237-264.
J.H. Bramble, J.E. Pasciak and O. Steinbach, On the stability of the L 2-projection on H 1 (),Math. Comp. 71(237) (2002) 147-156.
S.C. Brenner and L.R. Scott, The Mathematical Theory of Finite Element Methods (Springer, Berlin, 1996).
Z. Cai, On the finite volume element method, Numer. Math. 58 (1991) 713-735.
Z. Cai, J. Mandel and S. McCormick, The finite volume element method for diffusion equations on general triangulations, SIAM J. Numer. Anal. 38 (1991) 392-402.
C. Carstensen, Quasi-interpolation and a posteriori error analysis in finite element methods, Math. Model. Numer. Anal. 33 (1999) 1187-1202.
P. Clément, Approximation by finite element functions using local regularization, RAIRO Anal. Numér. 9 (1975) 77-85.
K. Eriksson, D. Estep, P. Hansbo and C. Johnson, Computational Differential Equations (Cambridge Univ. Press, Cambridge, 1996).
K. Eriksson and C. Johnson, An adaptive finite element method for linear elliptic problems, Math. Comp. 50 (1988) 361-382.
R.E. Ewing, R.D. Lazarov and Y. Lin, Finite volume element approximations for non-local reactive flows in porous media, Numer. Methods Partial Differential Equations 16 (2000) 285-311.
T. Ikeda, Maximum principle in finite element models for convection-diffusion phenomena, in: Lecture Notes in Numerical Applied Analysis, Vol. 4 (North-Holland, Amsterdam, 1983).
C. Johnson, Numerical Solution of Partial Differential Equations by the Finite Element Method (Cam-bridge Univ. Press, Cambridge, 1995).
R.D. Lazarov, J.E. Pasciak and S.Z. Tomov, Error control, local grid refinement and efficient solution algorithms for singularly perturbed problems, in: Analytical and Numerical Methods for Convection-.R. Lazarov, S. Tomov / A posteriori error estimates for finite volume method 503 Dominated and Singularly Perturbed Problems, eds. L.G. Vulkov, J.J.H. Miller and G.I. Shishkin (NOVA Science, 2000) pp. 71-82.
R.H. Li and Z.Y. Chen, The Generalized Difference Method for Differential Equations (Jilin Univ. Publ. House, 1994).
I.D. Mishev, Finite volume methods on Voronoi meshes, Numer. Methods Partial Differential Equations 14 (1998) 193-212.
R. Rodriguez, Some remarks on Zienkiewicz-Zhu estimator, Numer. Methods Partial Differential Equations 10 (1994) 625-635.
H.-O. Roos, M. Stynes and L. Tobiska, Numerical Methods for Singularly Perturbed Differential Equations (Springer, Berlin, 1996).
A.A. Samarskii, The Theory of Difference Schemes (Marcel Dekker, New York, 2001).
M. Slodicka and R. Van Keer, A nonlinear elliptic equation with non-local boundary condition solved by linearization, Preprint 1, Department of Mathematics, University of Gent, Belgium (2000).
M. Tabata, A finite element approximation corresponding to the up-wind finite differencing, Mem. Numer. Math. 4 (1977) 47-63.
S.Z. Tomov, Tool-box for parallel adaptive computations of 3-D convection-diffusion problems using domain decomposition, Technical Report ISC-00-10-MATH, Texas A&M University (2000).
R. Verfürth, A Review of a Posteriori Error Estimators and Adaptive Mesh Refinement Techniques (Teubner/Wiley, Stuttgart, 1996).
R. Verfürth, A posteriori error estimation and adaptive mesh-refinement techniques, J. Comput. Appl. Math. 50 (1994) 67-83.
J. Xu and L. Zikatanov, A monotone finite element scheme for convection-diffusion equations, Math. Comp. 68 (1999) 1429-1447.
O.C. Zienkiewicz and J.Z. Zhu, A simple error estimator and adaptive procedure for practical engi-neering analysis, Internat. J. Numer. Methods Engrg. 24 (1987) 337-357.
O.C. Zienkiewicz and J.Z. Zhu, Adaptivity and mesh generation, Internat. J. Numer. Methods Engrg. 32 (1991).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Lazarov, R., Tomov, S. A Posteriori Error Estimates for Finite Volume Element Approximations of Convection–Diffusion–Reaction Equations. Computational Geosciences 6, 483–503 (2002). https://doi.org/10.1023/A:1021247300362
Issue Date:
DOI: https://doi.org/10.1023/A:1021247300362