Abstract
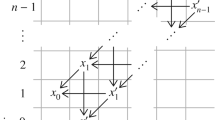
A diagram D of a knot defines the corresponding Gauss Diagram G D . However, not all Gauss diagrams correspond to the ordinary knot diagrams. From a Gauss diagram G we construct closed surfaces F G and S G in two different ways, and we show that if the Gauss diagram corresponds to an ordinary knot diagram D, then their genus is the genus of the canonical Seifert surface associated to D. Using these constructions we introduce the virtual canonical genus invariant of a virtual knot and find estimates on the number of alternating knots of given genus and given crossing number.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bacher, R. and Vdovina, A.: Counting 1-vertex triangulations of oriented surfaces, Institut Fourier preprint 447 (1998), available from http://www-fourier.ujf-grenoble.fr/.
Crowell, R.: Genus of alternating link types, Ann. of Math. (2) 69 (1959), 258–275.
Culler, M.: Using surfaces to solve equations in free group, Topology 20(2) (1981), 133–145.
Goussarov, M., Polyak, M. and Viro, O.: Finite-type invariants of classical and virtual knots, Topology 39(5) (2000), 1045–1068.
Kauffman, L. H.: Virtual knot theory, Europ. J. Combin. 20 (1999), 663–690.
Kawauchi, A.: On coefficient polynomials of the skein polynomial of an oriented link, Kobe J. Math. 11(1) (1994), 49–68.
Kobayashi, M. and Kobayashi, T.: On canonical genus and free genus of knot, J. Knot Theory Ramifications 5(1) (1996), 77–85.
Moriah, Y.: On the free genus of knots, Proc. Amer. Math. Soc. 99(2) (1987), 373–379.
Mosher, L.: A User's Guide to the Mapping Class Group: Once Punctured Surfaces, DIMACS Ser. 25, Amer. Math. Soc., Providence, 1994.
Menasco, W. W. and Thistlethwaite, M. B.: The Tait flyping conjecture, Bull. Amer. Math. Soc. 25(2) (1991), 403–412.
Murasugi, K.: On the genus of the alternating knot, J. Math. Soc. Japan 10 (1958), 94–105, 235-248.
Rolfsen, D.: Knots and Links, Math. Lecture Ser. 7, Publish or Perish, Berkeley, CA 1976.
Stoimenow, A.: Knots of genus one, to appear in Proc. Amer. Math. Soc.
Stoimenow, A.: Jones polynomial, genus and weak genus of a knot, Ann. Fac. Sci. Toulouse 8 (4) (1999), 677–693.
Vdovina, A.: Constructing orientable Wicks forms and estimation of their number, Comm. Algebra 23(9) (1995), 3205–3222.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Stoimenow, A., Tchernov, V. & Vdovina, A. The Canonical Genus of a Classical and Virtual Knot. Geometriae Dedicata 95, 215–225 (2002). https://doi.org/10.1023/A:1021211008278
Issue Date:
DOI: https://doi.org/10.1023/A:1021211008278