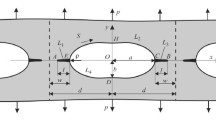
Abstract
We deduce computational formulas for the initial angle of propagation of quasibrittle fracture and the ultimate uniform load applied to a homogeneous isotropic linearly elastic plane weakened by an arbitrarily oriented curvilinear rounded notch. By using the conditions of maximum of the quantities appearing in the proposed criterion, we establish, for the first time, the relationships between the parameters of this formula. For some special cases, these parameters can be found and the influence of curvature at the tip of the defect and various mechanisms of fracture of the plate can be clarified. We also studied the onset of fracture for cracks propagating according to the criteria of maximum tangential stresses τmax, maximum specific energy of shaping W f, and maximum specific total energy W.
Similar content being viewed by others
REFERENCES
L. T. Berezhnyts'kyi, P. S. Kachur, and L. P. Mazurak, “On the theory of stress concentrators with rounded tips,” Fiz.-Khim. Mekh. Mater., 25, No. 5, 28–41 (1989).
L. T. Berezhnyts'kyi, “Method of perturbation of the shape of the boundary in fracture mechanics. Part 3: Cracklike defects in thin gently sloping shells,” Fiz.-Khim. Mekh. Mater., 34, No. 1, 44–54 (1998).
M. M. Senyuk and L. T. Berezhnyts'kyi, “Stretching of a microinhomogeneous body containing a cracklike arbitrarily oriented defect,” Fiz.-Khim. Mekh. Mater., 34, No. 3, 118–120 (1998).
V. V. Panasyuk and L. T. Berezhnyts'kyi, “Determination of the ultimate forces in a plate weakened by an arcwise crack in tension,” Fiz.-Khim. Mekh. Mater., 1, No. 3, 3–19 (1964).
L. T. Berezhnyts'kyi, L. P. Mazurak, and M. V. Delyavskii, “On the theory of pointed defects with various types of angular cuspidal points,” Fiz.-Khim. Mekh. Mater., 13, No. 4, 71–77 (1977).
L. T. Berezhnyts'kyi, M. V. Delyavskii, and V. V. Panasyuk, Bending of Thin Plates with Cracklike Defects [in Russian], Naukova Dumka, Kiev (1979).
L. P. Mazurak and L. T. Berezhnyts'kyi, Bending of Transversely Isotropic Plates with Cracklike Defects [in Russian], Naukova Dumka, Kiev (1979).
L. T. Berezhnyts'kyi and V. M. Sadivskii, “Limiting equilibrium of an orthotropic cracked plate,” Probl. Prochn., No. 12, 25–26 (1984).
V. V. Panasyuk, L. T. Berezhnyts'kyi, and R. S. Hromyak, “On the influence of the structure of materials on the propagation of cracks in tension,” Dokl. Akad. Nauk Ukr. SSR, Ser. A, No. 9, 811–816 (1976).
V. V. Panasyuk, L. T. Berezhnyts'kyi, and R. S. Hromyak, “On the influence of the structure of materials on the propagation of cracks in compression,” Dokl. Akad. Nauk Ukr. SSR, Ser. A, No. 10, 921–926 (1976).
V. V. Panasyuk and L. T. Berezhnyts'kyi, “Limiting equilibrium of plates with sharp stress concentrators,” Fiz.-Khim. Mekh. Mater., 1, No. 4, 424–434 (1965).
L. T. Berezhnyts'kyi, “Propagation of cracks appearing on the contour of a curvilinear hole in a plate,” Fiz.-Khim. Mekh. Mater., 2, No. 1, 21–31 (1966).
L. T. Berezhnyts'kyi, “Graphical interpretation of the stress intensity factors and the evaluation of the brittle strength of structural elements with cracklike defects,” Fiz.-Khim. Mekh. Mater., 13, No. 5, 27–31 (1977).
V. V. Panasyuk, Limiting Equilibrium of Brittle Bodies with Cracks [in Russian], Naukova Dumka, Kiev (1968).
K. Palaniswamy and W. G. Knauss, “On the problem of crack extension in brittle solids under general loading,” in: S. Nemt-Nasser (editor), Mechanics Today, Vol. 4, Pergamon Press, New York (1978), pp. 87–148.
A. A. Chizhik, “Crack resistance of materials for power machine building under the conditions of longitudinal shear,” Trudy TsKTI, No. 177, 3–17 (1980).
S. Ya. Yarema and H. S. Ivanitskaya, “Limiting equilibrium and propagation of oblique cracks. Survey of criteria,” Fiz.-Khim. Mekh. Mater., 22, No. 1, 45–57 (1986).
O. E. Andreikiv, Ya. L. Ivanyts'kyi, and Yu. Yu. Varyvoda, “KRT-criterion for cracked bodies in complex stressed states,” Dop. Akad. Nauk Ukr. RSR, No. 2, 37–39 (1987).
K. Hellan, Introduction to Fracture Mechanics, McGraw-Hill, New York (1984).
V. V. Panasyuk, Mechanics of Quasibrittle Fracture of Materials [in Russian], Naukova Dumka, Kiev (1991).
V. V. Panasyuk, “Some problems of fracture mechanics and strength of materials,” in: Fracture Mechanics of Materials and Strength of Structures [in Ukrainian], Issue 2, Vol. 1, Kamenyar, Lviv (1999), pp. 9–20.
I. É. Chaplya, L. T. Berezhnyts'kyi, and V. V. Panasyuk, “On the propagation of stresses and displacements near a crack in a homogeneous body with rectilinear anisotropy of the general form,” Fiz.-Khim. Mekh. Mater., 18, No. 4, 61–69 (1982).
K. F. Fischer, “Critique on fracture criteria in mixed-mode loading,” Theor. Appl. Fract. Mech., No. 3, 85–95 (1985).
G. P. Cherepanov, Mechanics of Brittle Fracture [in Russian], Nauka, Moscow (1974).
J. C. Williams and P. D. Ewing, “Fracture under complex stress-the angle crack problem,” Int. J. Fract. Mech., 8, No. 4, 441–446 (1972).
L. T. Berezhnyts'kyi and R. S. Hromyak, “Evaluation of the ultimate state of the matrix in the vicinity of a pointed rigid inclusion,” Fiz.-Khim. Mekh. Mater., 13, No. 2, 39–47 (1977).
L. P. Pook, “The effect of crack angle on fracture toughness,” Eng. Fract. Mech., 3, 205–218 (1971).
D. G. Smith and C. W. Smith, “Photoelastic determination of mixed-mode stress intensity factors,” Eng. Fract. Mech., 4, No. 2, 357–366 (1972).
G. C. Sih, “A special theory of crack propagation.-Methods of analysis and solutions of crack problems,” in: G. C. Sih (editor), Mechanics of Fracture, Noordhoff, Leyden (1973), pp. 21–45.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Berezhnyts'kyi, L.T. Arbitrarily Oriented Rounded Hole in a Linearly Elastic Plate. Materials Science 38, 185–197 (2002). https://doi.org/10.1023/A:1020981802081
Issue Date:
DOI: https://doi.org/10.1023/A:1020981802081