Abstract
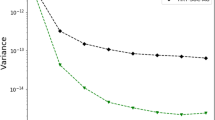
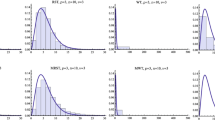
We propose a new methodology for modeling and analyzing power-tail distributions, such as the Pareto distribution, in communication networks. The basis of our approach is a fitting algorithm which approximates a power-tail distribution by a hyperexponential distribution. This algorithm possesses several key properties. First, the approximation can be achieved within any desired degree of accuracy. Second, the fitted hyperexponential distribution depends only on a few parameters. Third, only a small number of exponentials are required in order to obtain an accurate approximation over many time scales. Once equipped with a fitted hyperexponential distribution, we have an integrated framework for analyzing queueing systems with power-tail distributions. We consider the GI/G/1 queue with Pareto distributed service time and show how our approach allows to derive both quantitative numerical results and asymptotic closed-form results. This derivation shows that classical teletraffic methods can be employed for the analysis of power-tail distributions.
Similar content being viewed by others
References
J. Abate, G. Choudhury and W. Whitt, Waiting-time tail probabilities in queues with long-tail service-time distributions, Queueing Systems 16 (1994) 311–338.
A. Andersen and B. Nielsen, A Markovian approach for modeling packet traffic with long-range dependence, IEEE J. Selected Areas Comm. 16(5) (1998) 749–763.
P. Billingsley, Convergence of Probability Measures (Wiley, New York, 1968).
O. Boxma, Fluid queues and regular variation, Performance Evaluation 27/28 (1996) 699–712.
O. Boxma and J. Cohen, The M/G/1 queue with heavy-tailed service time distribution, IEEE J. Selected Areas Comm. 16(5) (1998) 719–732.
F. Brichet, J. Roberts, A. Simonian and D. Veitch, Heavy traffic analysis of a storage model with long range dependent on/off sources, Queueing Systems 23 (1996) 197–215.
J. Cohen, Some results on regular variation for distributions in queueing and fluctuation theory, J. Appl. Probab. 10 (1973) 343–353.
J. Cohen, The Single Server Queue, 2nd ed. (North-Holland, Amsterdam, 1982).
A. Feldmann and W. Whitt, Fitting mixture of exponentials to long-tail distributions to analyze network performance models, Performance Evaluation 31 (1998) 245–279.
W. Feller, An Introduction to Probability Theory and Its Applications, Vol. II, 2nd ed. (Wiley, New York, 1971).
M. Greiner, M. Jobmann and C. Klüppelberg, Telecommunication traffic, queueing models, and subexponential distributions, Queueing Systems 33(1-3) (1999) 125–152.
M. Greiner, M. Jobmann and L. Lipsky, The importance of power-tail distributions for telecommunication traffic models, Oper. Res. 47(2) (1999) 313–326.
N. Johnson and S. Kotz, Continuous Univariate Distributions-1 (Wiley, New York, 1970).
G. Latouche and V. Ramaswami, Introduction to Matrix Analytic Methods in Stochastic Modeling (SIAM, Philadelphia, PA, 1999).
W. Leland, M. Taqqu, W. Willinger and D. Wilson, On the self-similar nature of Ethernet traffic (extended version), IEEE/ACM Trans. Networking 2(1) (1994) 1–15.
L. Lipsky, Queueing Theory: A Linear Algebraic Approach (McMillan, New York, 1992).
B. Mandelbrot, A fast fractional Gaussian noise generator, Water Ressources Res. 7(3) (1971) 543–553.
A. Pakes, On the tails of waiting-time distributions, J. Appl. Probab. 12 (1975) 555–564.
S. Resnick and G. Samorodnitsky, Fluid queues, leaky buckets, on-off processes and teletraffic modeling with highly variable and correlated inputs, in: Self-Similar Network Traffic and Performance Evaluation, eds. K. Park and W. Willinger (Wiley, New York, 1998).
S. Robert and J.-Y. Le Boudec, New models for pseudo self-similar traffic, Performance Evaluation 30 (1997) 57–68.
M. Roughan, D. Veitch and M. Rumsewicz, Computing queue-length distributions for power-law queues, in: '98, San Francisco (March 1998).
D. Starobinski, Quality of service in high speed networks with multiple time-scale traffic, Ph.D. dissertation, Technion - Israel Institute of Technology, Haifa, Israel (May 1999).
D. Starobinski and M. Sidi, Stochastically bounded burstiness for communication networks, IEEE Trans. Inform. Theory 46(1) (2000) 206–212.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Starobinski, D., Sidi, M. Modeling and analysis of power-tail distributions via classical teletraffic methods. Queueing Systems 36, 243–267 (2000). https://doi.org/10.1023/A:1019195522806
Issue Date:
DOI: https://doi.org/10.1023/A:1019195522806