Abstract
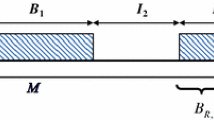
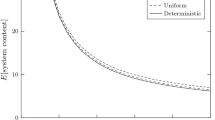
Recently it has been reported that various traffic exhibit long‐range dependence and/or self‐similarity. However, there exist some reports which suggest that traffic may be non‐stationary. In this paper we discuss the average overflow probability JN L(Ly)≡E[N−1Σn=1 NI{Qn L>Ly}] in a finite period [1,N] for a discrete‐time queue Qn L with a non‐stationary multiplexed input from L sources. By using the large deviation principle, we analyze the asymptotic behavior of JN L(Ly) as L increases and obtain an approximation formula of the form Jn L(Ly)≈C(L,y) e−γ(y). We apply the approximation formula to two examples. One is a non‐stationary process with deterministic level shifts and the other is a Gaussian process with spectrum of the form f−ν. The latter is non‐stationary if ν≥1.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
J. Beran, Statistics for Long-memory Processes (Chapman & Hall, London, 1994).
R.N. Bhattacharya, V.K. Gupta and E. Waymire, The Hurst effect under trends, Journal of Applied Probability 20 (1983) 649–662.
D.D. Botvich and N.G. Duffield, Large deviations, the shape of the loss curve, and economies of scale in large multiplexers, Queueing Systems 20 (1995) 293–320.
N.R. Chaganty and J. Sethuraman, Strong large deviation and local limit theorems, The Annals of Probability 21(3) (1993) 1671–1690.
A. Dembo and O. Zeitouni, Large Deviations Techniques and Applications (Jones and Bartlett, 1993).
N.G. Duffield, J.T. Lewis, N. O'Connell, R. Russell and F. Toomey, Predicting quality of service for traffic with long-range dependence, in: Proc. of IEEE ICC'95, Seattle (1995) pp. 473–477.
N.G. Duffield and N. O'Connell, Large deviations and overflow probabilities for the general single-server queue, with applications, Mathematical Proceedings of the Cambridge Philosophical Society 118 (1995) 363–374.
K. Kobayashi and Y. Takahashi, Tail probability of a Gaussian fluid queue under finite measurement of input processes, in: Performance and Management of Complex Communication Networks, eds. H. Takagi and Y. Takahashi (Chapman & Hall, London, 1998) pp. 43–58.
K. Kobayashi, S. Kudoh, H. Takagi, G. Hamada and F. Kubota, Self-similarity of MPEG2 video traffic through spectral analysis, in: Proc. of Symposium on Performance Models for Information Communication Networks, Kyoto (1998) pp. 211–219.
M. Montgomery and G. De Veciana, On the relevance of time scales in performance oriented traffic characterizations, in: Proc. of IEEE INFOCOM, San Francisco (1996) pp. 4d.3.1–4d.3.8.
H. Takayasu, Fractals in the Physical Sciences (Wiley, New York, 1989).
W. Willinger, Self-similar traffic flows in high-speed networks: measurements, inference and modeling, PMCCN'97 tutorial document (1997).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kobayashi, K., Takahashi, Y. Overflow probability for a discrete‐time queue with non‐stationary multiplexed input. Telecommunication Systems 15, 157–166 (2000). https://doi.org/10.1023/A:1019134726750
Issue Date:
DOI: https://doi.org/10.1023/A:1019134726750