Skip to main content
SpringerLink
Log in

Modeling of Bonding at an Interface Crack

  • Published:
International Journal of Fracture Aims and scope Submit manuscript

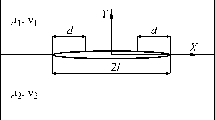
Abstract

A mechanical and mathematical model is suggested for an interface crack with bonding in its end zones. Normal and shear bond tractions occurring under the action of the external loads are searched for by solving a system of two singular integrodifferential equations. The stress intensity factors at the crack tip are calculated taking the compensating action of the bonds into account. Energetic characteristics of the interface crack (the deformation energy release rate and the rate of the energy absorption by the bonds) are analyzed. A sensitivity analysis is performed of the force and energetic characteristics of the interface crack to the end zone size, bond compliance and limit stretching.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Barenblatt, G.I. (1959a). The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks. Journal of Applied Mathematics and Mechanics 23(3), 434-444.

    Article  MATH  MathSciNet  Google Scholar 

  • Barenblatt, G.I. (1959b). The formation of equilibrium cracks during brittle fracture. Rectilinear cracks in plane plates. Journal of Applied Mathematics and Mechanics 23(4), 706-721.

    Article  MATH  MathSciNet  Google Scholar 

  • Barenblatt, G.I. (1959c). The formation of equilibrium cracks during brittle fracture. Stability of isolated cracks. Connections with the energetic theories. Journal of Applied Mathematics and Mechanics 23(5), 893-900.

    Article  MATH  MathSciNet  Google Scholar 

  • Barenblatt, G.I. (1962). The mathematical theory of equilibrium cracks in brittle fracture. Advances in Applied Mechanics (Edited by H.L. Dryden and T. von Karman), Academic Press, New York, 55-129.

    Google Scholar 

  • Budiansky, B. and Cui, Y.L. (1994). On the tensile strength of a fiber-reinforced ceramic composite containing a crack-like flaw. Journal of Mechanics and Physics of Solids 42(1), 1-19.

    Article  MATH  MathSciNet  ADS  Google Scholar 

  • Brown, H.B. (1994). Adhesion between polymers. IBM Journal Research and Developments 38, 379-389.

    Google Scholar 

  • Carpinteri, A. and Massabo, R. (1996). Bridged versus cohesive crack in the flexural behavior of brittle-matrix composites. International Journal of Fracture 81(2), 125-145.

    Article  Google Scholar 

  • Cox, B.N. and Marshall, D.B. (1994). Concepts for bridged cracks in fracture and fatique. Acta Metallurgica Materialia 42(2), 341-363.

    Article  Google Scholar 

  • Erdogan, F., Gupta, G.D. and Cook, T.S. (1977). Numerical solution of singular integral equations. Mechanics of Fracture, Vol. 1: Methods of Analysis and Solutions of Crack Problems, 368-425.

  • Entov, V.M. and Salganik, R.L. (1968). On the Prandtl model of brittle fracture. Inzhenernyi Zhurnal, MTT [J. of Engineering, Mechanics of Solids] (11), 87-99.

    Google Scholar 

  • Goldstein, R.V. and Perelmuter, M.N. (1996). Interface Cracks with Bonding. Institute for Problems in Mechanics, Russian Academy of Sciences, Moscow, Preprint N 568.

    Google Scholar 

  • Hong, Ji and de Gennes, P.-G. (1993). Adhesion via connector molecules: The many-stitch problem. Macromolecules 26, 520-525.

    Article  ADS  Google Scholar 

  • Hutchinson, J.W. and Suo, Z. (1990). Mixed mode cracking in layered materials. Advances in Applied Mechanics (Edited by J.W. Hutchinson and T.Y. Wu) 28.

  • Kurtz, R.D., Farris, T.N. and Sun, C.T. (1994). The numerical solution of Cauchy singular integral equations with application to fracture. International Journal of Fracture 66, 139-154.

    Article  ADS  Google Scholar 

  • Rice, J.R. and Sih, G.C. (1965). Plane problems of cracks in dissimilar media. Journal of Applied Mechanics 32, 418-423.

    Google Scholar 

  • Rice, J.R. (1988). Elastic fracture mechanics concepts for interface cracks. Journal of Applied Mechanics 55, 98-103.

    Article  Google Scholar 

  • Rose, L.R.F. (1987). Crack reinforcement by distributed springs. Journal of Mechanics and Physics of Solids 35, 383-405.

    Article  MATH  ADS  Google Scholar 

  • Salganik, R.L. (1963). On brittle fracture of glued bodies. Journal of Applied Mathematics and Mechanics 27(5), 957-962.

    Article  Google Scholar 

  • Segerlind, L.J. (1976). Applied Finite Element Analysis, Wiley, N.Y.-London.

    MATH  Google Scholar 

  • Slepijn, L.I. (1981). Mechanics of Cracks. Sydostroenie, Leningrad.

    Google Scholar 

  • Weitsman, Y. (1986). Nonlinear analysis of crazes. Journal of Applied Mechanics 53, 97-102.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Russian Academy of Sciences, Institute for Problems in Mechanics, pr. Vernadskogo, 101, 117526, Moscow, Russia

    Robert Goldstein & Michail Perelmuter

Authors
  1. Robert Goldstein
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michail Perelmuter
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Goldstein, R., Perelmuter, M. Modeling of Bonding at an Interface Crack. International Journal of Fracture 99, 53–79 (1999). https://doi.org/10.1023/A:1018382321949

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1018382321949

Search

Navigation