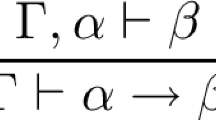Abstract
The author presents a deduction system for Quantum Logic. This system is a combination of a natural deduction system and rules based on the relation of compatibility. This relation is the logical correspondant of the commutativity of observables in Quantum Mechanics or perpendicularity in Hilbert spaces.
Contrary to the system proposed by Gibbins and Cutland, the natural deduction part of the system is pure: no algebraic artefact is added. The rules of the system are the rules of Classical Natural Deduction in which is added a control of contexts using the compatibility relation.
The author uses his system to prove the following theorem: if propositions of a quantum logical propositional calculus system are mutually compatible, they form a classical subsystem.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
N. J. Cutland and P. F. Gibbins, “A Regular Sequent Calculus for Quantum Logic in which 2227 and 2228 are Dual”, Logique et Analyse 99(1982), pages 221–248.
P. F. Gibbins, “A User-friendly Quantum Logic”, Logique et Analyse 112(1985), pages 353–362.
J.-Y. Girard, Linear Logic, Theoretical Computer Science 50(1987), pages 1–102.
C. Piron, “Axiomatique Quantique”, Helvetica Physica Acta 37(1964), pages 439–468.
J. von Neumann and G. Birkhoff, “The Logic of Quantum Mechanics”, Annals of Mathematics 37(1936), pages 823–834.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Delmas-Rigoutsos, Y. A Double Deduction System for Quantum Logic Based On Natural Deduction. Journal of Philosophical Logic 26, 57–67 (1997). https://doi.org/10.1023/A:1017941704456
Issue Date:
DOI: https://doi.org/10.1023/A:1017941704456