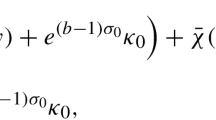Abstract
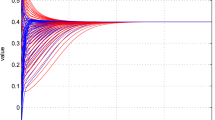
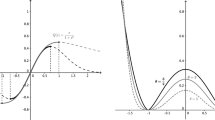
We consider nearly spherically symmetric expanding fronts in the scalar bistable reaction-diffusion equation on RN. As t→∞, the front is known to look more and more like a sphere under the rescaling of the radius to unity. In this paper we prove that, if the initial state is spherically symmetric and approximated by a one-dimensional traveling wave with a sufficiently large radius, then the solution is approximated uniformly for all t≥0 without the rescaling of the radius by the one-dimensional traveling wave with the speed of V=c−(N−1)κ, where c>0 is the speed of the one-dimensional traveling wave solution and κ the mean curvature of the sphere. We further show that, if the initial state is a slightly perturbed one from the spherical front, the difference between the actual front and the expanding sphere hardly grows or decays for all t≥0, although the relative magnitude of the perturbation to the radius of the sphere decreases to zero.
Similar content being viewed by others
REFERENCES
Aronson, D. G., and Caffarelli, L. A. (1983). The initial trace of a solution of the porous medium equation. Trans. AMS 280, 351-366.
Aronson, D. G., and Weinberger, H. F. (1978). Multidimensional nonlinear diffusion arising in population genetics. Adv. Math. 30, 33-76.
Barles, G., and Souganidis, P. E. (1998). A new approach to front propagation problems. Arch. Rational Mech. Anal. 141, 237-296.
Barles, G., Soner, H. M., and Souganidis, P. E. (1993). Front propagation and phase field theory. SIAM J. Control Optim. 31, 439-469.
Bronsard, L., and Kohn, R. V. (1991). Motion by mean curvature as the singular limit of Ginzburg-Landau dynamics. J. Diff. Eqs. 90, 211-237.
Caginalp, G., and Fife, P. C. (1987). Elliptic problems involving phase boundaries satisfying a curvature condition. IMA J. Appl. Math. 38, 195-217.
Carr, J., and Pego, R. L. (1989). Metastable patterns in solutions of u t=ε2 u xx-f(u). CPAM 42, 523-576.
Carr, J., and Pego, R. (1990). Invariant manifolds for metastable patterns in u t=ε2 u xx-f(u). Proc. Roy. Soc. Edinburgh A 116, 133-160.
Chen, X. (1992). Generation and propagation of interfaces for reaction-diffusion equations. J. Diff. Eqs. 96, 116-141.
de Mottoni, P., and Schatzman, M. (1995). Geometrical evolution of developed interfaces. Trans. AMS 347, 1533-1589.
Ei, S.-I., and Yanagida, E. (1998). Slow dynamics of interfaces in the Allen-Cahn equation on a strip-like domain. SIAM J. Math. Anal. 29, 555-595.
Ei, S.-I., Iida, M., and Yanagida, E. (1997). Dynamics of interfaces in a scalar parabolic equation with variable diffusion coefficients. Japan J. Indust. Appl. Math. 14, 1-23.
Evans, L. C., Soner, H. M., and Souganidis, P. E. (1992). Phase transitions and generalized motion by man curvature. CPAM 45, 1097-1123.
Fife, P. C. (1988). Dynamics of Internal Layers and Diffusive Interfaces, SIAM, Philadelphia.
Fife, P. C., and Greenlee, W. M. (1974). Interior transition layers for elliptic boundary value problems with a small parameter. Russ. Math. Surv. 29, 103-131.
Fife, P. C., and McLeod, J. B. (1977). The approach of solutions of nonlinear diffusion equations to traveling front solutions. Arch. Ration. Mech. Anal. 65, 335-361.
Fusco, G. (1990). A geometric approach to the dynamics of u t=ε2 u xx+f(u) for small ? In Kirchgassner, K. (ed.), Problems Involving Change of Type, Springer-Verlag, New York, pp. 53-73.
Fusco, G., and Hale, J. K. (1989). Slow-motion manifolds, dormant instability, and singular perturbations. J. Dynam. Diff. Eqs. 1, 75-94.
Fusco, G., Hale, J. K., and Xun, J. (1996). Traveling waves as limits of solutions on bounded domains. SIAM J. Math. Anal. 27, 1544-1558.
Ilmanen, T. (1993). Convergence of the Allen-Cahn equation to Brakke's motion by mean curvature. J. Diff. Geom. 38, 417-461.
Jones, C. K. R. T. (1983). Asymptotic behaviour of a reaction-diffusion equation in higher space dimensions. Rocky Mt. J. Math. 13, 355-364.
Kohn, R. V., and Sternberg, P. (1989). Local minimizers and singular perturbations. Proc. Roy. Soc. Edinburgh A 111, 69-84.
Matano, H. (1983). Asymptotic behavior of the free boundaries arising in one phase Stefan problems in multi-dimensional spaces. In Fujta, H., Lax, P. D., and Strang, G. (eds.), Nonlinear Partial Differential Equations in Applied Science, North-Holland, Amsterdam, pp. 133-151.
Schneider, G. (1996). The validity of generalized Ginzburg-Landau equations. Math. Methods Appl. Sci. 19, 717-736.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Yagisita, H. Nearly Spherically Symmetric Expanding Fronts in a Bistable Reaction-Diffusion Equation. Journal of Dynamics and Differential Equations 13, 323–353 (2001). https://doi.org/10.1023/A:1016632124792
Issue Date:
DOI: https://doi.org/10.1023/A:1016632124792