Skip to main content
SpringerLink
Log in

Two Typical Steady-State Bifurcations for Time-Reversible Vector Field Families

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

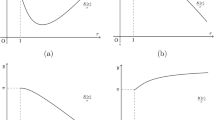
Two typical steady-state bifurcations for time-reversible vector field families are studied, including allowance for a nontrivial nullspace forced by time-reversal symmetry. Under certain nondegeneracy conditions, it is shown that either a non- time-symmetric pitchfork or a time-symmetric transcritical bifurcation occurs. The method is extended to the equivariant case and applied by way of example to a class of time-reversible problems with Dn×O(2) symmetries which includes the particle sedimentation model known as the Stokeslet model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. Arnold, V. I. (1988). Geometrical Methods in the Theory of Ordinary Differential Equations, 2nd Ed., Springer-Verlag, New York.

    Google Scholar 

  2. Caflisch, R., Lim, C. C., Luke, J. H. C, and Sangani, A. S. (1988). Periodic solutions of three sedimenting particles. Phys. Fluids 31(11), 3175-3179.

    Google Scholar 

  3. Golubitsky, M., Krupa, M., and Lim, C. (1990). Time-reversibility and particle sedimentation. SIAM J. Appl. Math. 51(1), 49-72.

    Google Scholar 

  4. Golubitsky, M., and Schaeffer, D. G. (1985). Singularities and Groups in bifurcation Theory: Vol. I, Appl. Math. Sci. 51, Springer-Verlag, New York.

    Google Scholar 

  5. Golubitsky, M., Stewart, I. N, and Schaeffer, D. G. (1988). Singularity and Groups in Bifurcation Theory: Vol. II, Appl. Math. Sci. 69, Springer-Verlag, New York.

    Google Scholar 

  6. McComb, I. (1993). Bifurcations of Time-Reversible, Equivariant Vector Field Families, Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, New York.

    Google Scholar 

  7. McComb, I, and Lim, C. C. (1993). Stability of a class of time-reversible, Dn × O(2)-symmetric homogeneous vector fields. SIAM J. Math. Anal. 24(4), 1009-1029.

    Google Scholar 

  8. McComb, I., and Lim, C. (1995). Resonant normal modes for time-reversible, equivariant vector fields. J. Dynam. diff. Eqs. 7(2), 287-339.

    Google Scholar 

  9. Politi, A, Oppo, G. L., and Baddi, R. (1986). coexistence of conservative and dissipative behavior in reversible dynamical systems. Phys. Rev. A 33(6), 4055-4060.

    Google Scholar 

  10. Sevryuk, M. (1986). Reversible Systems, Lecture Notes in Mathematics 1211, Springer-Verlag, Berlin.

  11. Teixeira, M. (1997). Singularities of reversible vector fields. Physica D 100, 101-118.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Rensselaer Polytechnic Institute, Troy, New York, 12180-3590

    Chjan C. Lim

  2. Department of Computational Science, National University of Singapore, Singapore

    Chjan C. Lim

  3. Monta Vista High School, Cupertino, California

    I-Heng McComb

Authors
  1. Chjan C. Lim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I-Heng McComb
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lim, C.C., McComb, IH. Two Typical Steady-State Bifurcations for Time-Reversible Vector Field Families. Journal of Dynamics and Differential Equations 13, 251–274 (2001). https://doi.org/10.1023/A:1016628023883

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1016628023883

Search

Navigation