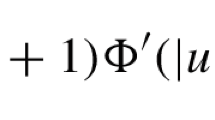Abstract
We consider the system of ordinary differential equations x = f(x,y), εy = g(x,y), where x ∈ℝ2, y ∈ ℝ, 0 <ε ≪ 1, and f,g ∈C∞. It is assumed that the equation g = 0 determines two different smooth surfaces y = ϕ(x) and y = ψ(x) intersecting generically along a curve l. It is further assumed that the trajectories of the corresponding degenerate system lying on the surface y = ϕ(x) are ducks, i.e., as time increases, they intersect the curve l generically and pass from the stable part {y =ϕ(x),g'y < 0} of this surface to the unstable part {y =ϕ(x),g'y > 0}. We seek a solution of the so-called “duck survival” problem, i.e., give an answer to the following question: what trajectories from the one-parameter family of duck trajectories for ɛ= 0 are the limits as ɛ → 0 of some trajectories of the original system.
Similar content being viewed by others
REFERENCES
E. F. Mishchenko, Yu. S. Kolesov, A. Yu. Kolesov, and N. Kh. Rozov, Periodic motions and Bifurcational Processes in Singularly Perturbed Systems [in Russian], Fizmatlit, Moscow, 1995.
A. Yu. Kolesov, E. F. Mishchenko, and N. Kh. Rozov, “Solution of singularly perturbed boundaryvalue problems by the “duck hunting” method, Trudy Mat. Inst. Steklov [Proc. Steklov Inst. Math.], 224 (1999), 187–207.
E. F. Mishchenko and N. Kh. Rozov, Differential Equations with a Small Parameter and Relaxation Oscillations [in Russian], Nauka, Moscow, 1975.
A. B. Vasil'eva and V. F. Butuzov, Asymptotic Expansions of Solutions of Singularly Perturbed Equations [in Russian], Nauka, Moscow, 1973.
V. A. Sobolevand E. A. Shchepakina, “Duck trajectories in a problem of combustion theory,” Differentsial' nye Uravneniya [Differential Equations], 32 (1996), no. 9, 1175–1184.
N. R. Lebovitz and R. J. Schaar, “Exchange of stabilities in autonomous systems,” Stud. Appl. Math., 54 (1975), 229–260.
V. A. Sobolev and E. A. Shchepakina, “Integral surfaces with a change in stability and duck trajectories,” Izv. RAEN. Ser. MMMIU, 1 (1997), no. 3, 176–187.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Bobkova, A.S., Kolesov, A.Y. & Rozov, N.K. The “Duck Survival” Problem in Three-Dimensional Singularly Perturbed Systems with Two Slow Variables. Mathematical Notes 71, 749–760 (2002). https://doi.org/10.1023/A:1015812727037
Issue Date:
DOI: https://doi.org/10.1023/A:1015812727037