On Mathematical Models of Average Flow in Heterogeneous Formations

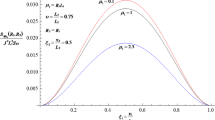
Abstract

We consider a general model of transient flow in media of random conductivity and storativity. The flow is driven by the spatially distributed source function φ(x, t) and the initial head distribution h ₀(x). The function φ models sources and wells and can be deterministic, random or a sum of both. The deterministic source function corresponds to singularities of deterministic strength, whereas the random φ models the head boundary condition. In the latter case, φ is shown to be proportional to the hydraulic conductivity. The aim of the study is to analyze the feasibility of averaging the flow equations and of developing the mathematical model of average flow (AFM) without solving problems in detail. It is shown that the problem of averaging is reduced to deriving two constitutive equations. The first equation, the effective Darcy's law (EDL) stems from averaging Darcy's law at local scale. The second one is related to the medium ability to store a fluid and expresses the correlation between the storativity and head in terms of the mean head. Both relationships are required to be completely determined by the medium structure (conductivity and storativity statistical properties) and independent of the flow configuration (functions φ and h ₀). We show that if one of the constitutive equations exists, the same is true respective to the second. This reduces the problem of averaging to the classic one of deriving the EDL. For steady flows the EDL is shown to exist for flows driven by sources (wells) of either deterministic flux or head boundary conditions. No EDL can be derived if both types of sources are present in the flow domain. For unsteady flows the EDL does not exist if the initial head correlates with the medium properties. For uncorrelated initial head distribution, its random residual (due to the measurement errors and scarcity of the data) has no impact on the EDL and is immaterial. For deterministic h ₀, the only case for which the EDL exists is the flow by sources of deterministic discharge. For sources of given head boundary condition the EDL can be derived only for uniform initial head distribution. For all other cases, the EDL does not exist. The results of the study are not limited by usually adopted assumptions of weak heterogeneity and of stationarity of the formation random properties.