Skip to main content
SpringerLink
Log in

Estimating the Firm Value Distribution Function by Entropy Optimization and Geometric Programming

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

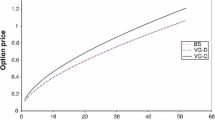
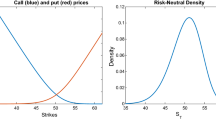
By applying the option pricing theory ideas, this paper models the estimation of firm value distribution function as an entropy optimization problem, subject to correlation constraints. It is shown that the problem can be converted to a dual of a computationally attractive primal geometric programming (GP) problem and easily solved using publicly available software. A numerical example involving stock price data from a Japanese company demonstrates the practical value of the GP approach. Noting the use of Monte Carlo simulation in option pricing and risk analysis and its difficulties in handling distribution functions subject to correlations, the GP based method discussed here may have some computational advantages in wider areas of computational finance in addition to the application discussed here.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. F. Black and M. Scholes, Pricing of options and corporate liabilities, Journal of Political Economy 81 (1973) 637–659.

    Google Scholar 

  2. P.P. Boyle, Options: A Monte Carlo approach, Journal of Financial Economics 4 (1977) 323–328.

    Google Scholar 

  3. P.W. Buchen and M. Kelly, The maximum entropy distribution of an asset inferred from option prices, Journal of Finance and Quantitative Analysis 31 (1996) 143–159.

    Google Scholar 

  4. A. Charnes, K.E. Haynes, F.Y. Phillips and G. White, New equivalences and dualities from the extremal solutions of the gravity models of spatial interaction; an approach using unconstrained dual of an extended geometric programming problem, Journal of Regional Sciences 17 (1977) 71–76.

    Google Scholar 

  5. J.M. Cozzolino and M.J. Zahner, The maximum entropy distribution of the future market price of a stock, Operations Research 21 (1973) 1200–1211.

    Google Scholar 

  6. P. Crosbie, Modeling default risk, in: Credit Derivatives-Trading & Management of Credit & Default Risk, ed. S. Das (Wiley, Singapore, 1998) pp. 299–315.

    Google Scholar 

  7. A. Damodaran, Investment Valuation-Tools and Techniques for Determining the Value of any Asset (Wiley, 1996).

  8. R.J. Duffin, E.L. Peterson and C. Zener, Geometric Programming-Theory and Applications (Wiley, New York, 1967).

    Google Scholar 

  9. P. Embrechts, A. McNeil and D. Straumann, Correlation: Pitfalls and alternatives, RISK (1999) 69-71.

  10. S.C. Fang, J.R. Rajasekera and H.S.J. Tsao, Entropy Optimization and Mathematical Programming (Kluwer Academic, 1997).

  11. R. Geske, Valuation of compound options, Journal of Financial Economics 7 (1979) 63–81.

    Google Scholar 

  12. J.M. Harrison, Brownian Motion and Stochastic Flow Systems (Wiley, 1985).

  13. J.C. Hull, Options, Futures, and Other Derivative Securities, 2nd ed. (Prentice-Hall, 1993).

  14. J.C. Jackwerth and M. Rubinstein, Recovering probability distributions from option prices, The Journal of Finance 51(5) (1996) 1611–1631.

    Google Scholar 

  15. E.T. Jaynes, Information theory and statistical mechanics, Physics Review 106 (1957) 620–630.

    Google Scholar 

  16. T.R. Jefferson and C.H. Scott, Entropy and geometric programming in transportation planning, Opsearch 15 (1978) 22–34.

    Google Scholar 

  17. J.N. Kapur, Maximum Entropy Models in Science and Engineering (Wiley, New Delhi, India, 1989).

    Google Scholar 

  18. I.J. Myung, S. Ramamoorti and A.D. Bailey, Maximum entropy aggregation of expert predictions, Management Science 42(10) (1996) 1420–1436.

    Google Scholar 

  19. T.R. Rockafellar, Convex Analysis (Princeton University Press, 1972).

  20. L. Schrage, Optimization Modeling with LINGO, LINDO Systems (January 1999).

  21. M. Stutzer, A simple nonparametric approach to derivative security valuation, Journal of Finance 51 (1996) 1633–1652.

    Google Scholar 

  22. M. Stutzer and M. Chowdhury, A simple nonparametric approach to bond futures option pricing, Journal of Fixed Income 8 (1999) 67–76.

    Google Scholar 

  23. M. Yamada and J.R. Rajasekera, Business activities evaluation analysis, Nikkei Financial (April 28, 1999) (in Japanese).

Download references

Author information

Authors and Affiliations

  1. Graduate School of International Management, International University of Japan, Yamato-machi, Niigata, 949-72, Japan

    J.R. Rajasekera

  2. Corporate Advisory Department, UFJ Capital Markets Securities Co., Ltd., Ote Center Bldg., 1-3, Otemachi 1-chome, Chiyoda-ku, Tokyo, 100-8138, Japan

    M. Yamada

Authors
  1. J.R. Rajasekera
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Yamada
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rajasekera, J., Yamada, M. Estimating the Firm Value Distribution Function by Entropy Optimization and Geometric Programming. Annals of Operations Research 105, 61–75 (2001). https://doi.org/10.1023/A:1013397314149

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1013397314149

Search

Navigation