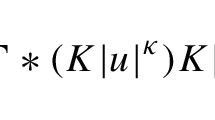Abstract
We generalize the Ostrohrads'kyi method for the construction of the Hamiltonian description of a nondegenerate (regular) variational problem of arbitrary order to the case of degenerate (singular) Lagrangians. These Lagrangians are of major interest in the contemporary theory of elementary particles. For simplicity, we consider the Hamiltonization of a variational problem defined by a singular second-order Lagrangian. Generalizing the Ostrohrads'kyi method, we derive equations of motion in the phase space. We determine a complete collection of constraints of the theory.
Similar content being viewed by others
REFERENCES
A. A. Slavnov and L. D. Faddeev, Introduction to the Quantum Theory of Gauge Fields [in Russian], Nauka, Moscow (1978).
M. Kaku, “Superconformal gravity in Hamiltonian form: Another approach to the renormalization of gravitation,” Phys. Rev. D, 27, No. 12, 2809-2818 (1983).
B. Podolsky and P. Schwed, “Review of generalized electrodynamics,” Rev. Mod. Phys., 20, No. 1, 40-50 (1948).
R. Utiyama and B. S. De Witt, “Renormalization of a classical gravitational field interacting with quantized matter fields,” J. Math. Phys., 3, No. 4, 608-618 (1962).
K. S. Stelle, “Renormalization of higher-derivative quantum gravity,” Phys. Rev. D, 16, No. 4, 953-969 (1997).
E. S. Fradkin and A. A. Tseytlin, “Renormalizable asymptotically free quantum theory of gravity,” Nucl. Phys. B, 201, No. 3, 469-491 (1982).
D. G. Boulware and S. Deser, “String generated gravity models,” Phys. Rev. Lett., 55, No. 24, 2656-2660 (1985).
B. Zwiebach, “Curvature squared terms and string theories,” Phys. Lett. B, 156, No. 5, 6, 315-317 (1985).
D. G. Boulware, “Quantization of higher derivative theories of gravity,” in: Quantum Theory of Gravity, Adam Hilger, Bristol (1984), pp. 267-294.
S. W. Hawking, “Who's afraid of (higher derivative) ghosts?,” in: Quantum Field Theory and Quantum Statistics, Vol. 2, Adam Hilger, Bristol (1987), pp. 129-139.
V. V. Nesterenko, “Curvature and torsion of the world curve in the action of the relativistic particle,” J. Math. Phys., 32, No. 12, 3315-3320 (1992).
V. V. Nesterenko, “Torsion in the action of the relativistic particle,” Class. Quant. Grav., 9, 1101-1114 (1992).
V. V. Nesterenko, “Canonical quantization of a relativistic particle with torsion,” Mod. Phys. Lett. A, 6, 719-726 (1991).
V. V. Nesterenko, “Relativistic particle with curvature in an external electromagnetic field,” Int. J. Mod. Phys. A, 6, 3989-3996 (1991).
V. V. Nesterenko, “On a model of a relativistic particle with curvature and torsion,” J. Math. Phys., 34, 5589-5595 (1993).
V. V. Nesterenko, “On squaring the primary constraints in a generalized Hamiltonian dynamics,” Phys. Lett. B, 327, 50-55 (1994).
M. S. Plyushchay, “Massive relativistic point particle with rigidity,” Int. J. Mod. Phys., 4, No. 15, 3851-3865 (1989).
M. S. Plyushchay, “Massless particle with rigidity as a model for the description of bosons and fermions,” Phys. Lett. B, 243, No. 4, 383-388 (1990).
M. S. Plyushchay, “The model of the relativistic particle with torsion,” Nucl. Phys. B, 362, No. 1, 2, 54-72 (1991).
Yu. A. Kuznetsov and M. S. Plyushchay, “The model of the relativistic particle with curvature and torsion,” Nucl. Phys., 389, No. 1, 181-205 (1993).
V. V. Nesterenko and Nguyen Swan Han, “The Hamiltonian formalism in the model of the relativistic string with rigidity,” Int. J. Mod. Phys., 3, No. 10, 2315-2329 (1988).
M. V. Ostrohrads'kyi, “A memoir on the differential equations related to an isoperimetric problem,” in: Complete Collection of Works [in Russian], Vol. 2, Ukrainian Academy of Sciences (1961), pp. 139-233. [see also Variational Principles of Mechanics [in Russian], Fizmatgiz, Moscow (1959), pp. 315–387.]
E. T. Whittaker, A Treatise of the Analytical Dynamics of Particles and Rigid Bodies, University Press, Cambridge (1927).
V. A. Dubrovin, S. P. Novikov, and A. T. Fomenko, Modern Geometry [in Russian], Nauka, Moscow (1979).
P. A. M. Dirac, Lectures on Quantum Mechanics, Belfer Graduate School of Science, Yeshiva University, New York (1964).
A. J. Hanson, T. Regge, and C. Teitelboim, Constrained Hamiltonian Systems, Acad. Naz. dei Lincei, Roma (1976).
V. V. Nesterenko and A. M. Chervyakov, Singular Lagrangians: Classical Dynamics and Quantization [in Russian], Preprint No. P2-86-323, Joint Institute for Nuclear Research, Dubna (1986).
D. M. Gitman and I. V. Tyutin, Canonical Quantization of Fields with Constraints [in Russian], Nauka, Moscow (1986).
B. M. Barbashov and V. V. Nesterenko, “Continuous symmetries in field theory,” Fortsch. Phys., 31, No. 10, 535-567 (1983).
V. V. Nesterenko and A. M. Chervyakov, “On some properties of constraints in theories with degenerate Lagrangians,” Teor. Mat. Fiz., 64, No. 1, 82-91 (1985).
C. Battle, J. Gomis, J. M. Pons, and N. Roman, “Lagrangian and Hamiltonian constraints,” Lett. Math. Phys., 13, No. 1, 17-23 (1987).
K. Kamimura, “Singular Lagrangian and constrained Hamiltonian systems, generalized canonical formalism,” Nuovo Cim. B, 68, No. 1, 33-54 (1982).
R. Pisarski, “Field theory of paths with a curvature-dependent term,” Phys. Rev. D, 34, No. 2, 670-673 (1986).
F. Alonso and D. Espriu, “On the fine structure of strings,” Nucl. Phys. B, 283, No. 3, 4 393-412 (1987).
P. A. Griffiths, Exterior Differential Systems and the Calculus of Variations, Birkhäuser, Berlin (1983).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Nesterenko, V.V. Ostrohrads'kyi Formalism for Singular Lagrangians with Higher Derivatives. Ukrainian Mathematical Journal 53, 1220–1236 (2001). https://doi.org/10.1023/A:1013391409148
Issue Date:
DOI: https://doi.org/10.1023/A:1013391409148