Abstract
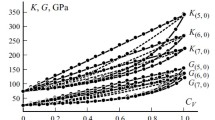
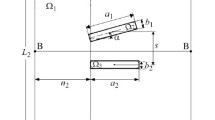
Eshelby's equivalent-inclusion method is extended to a finite number of arbitrarily oriented anisotropic ellipsoidal inclusions in an elastic isotropic matrix under polynomial mechanical loading and heating. The interaction of two identical and two different triaxial ellipsoidal inclusions in an elastic medium is studied as numerical examples. In special cases, the results are compared with those obtained by other authors
Similar content being viewed by others
REFERENCES
V. S. Kirilyuk, “On the structure of stresses inside an ellipsoidal heterogeneity for thermoelastic problems', ” Vych. Prikl. Mat., Issue 71, 70–76 (1990).
V. S. Kirilyuk, “On the thermostressed state of an ellipsoidal heterogeneity (inclusion) under polynomial mechanical and thermal external fields', ” Teor. Prikl. Mekh., 30, 67–76 (1999).
V. I. Kushch, “Summation theorems for partial vector solutions of the Lamé equation in a spheroidal basis', ” Prikl. Mekh., 31, No. 2, 86–92 (1995).
V. I. Kushch, The Stress State and Macroscopic Properties of Partially Homogeneous Bodies with Spheroidal Interfaces [in Ukrainian], Doctoral Thesis, Kiev (1998).
H. Neuber, Kerbspannungslehre (Theory of Notch Stress Concentration), Springer Verlag, Berlin—Heidelberg—New York—Tokyo (1985).
A. G. Nikolaev, “Formulas for reexpansion of vector solutions of the Lamé equation in spherical and spheroidal coordinate systems', ” Mat. Metod. Analiza Dinam. Sistem, 8, 100–104 (1984).
A. G. Nikolaev and V. S. Protsenko, “The first and second axisymmetric problems of elastic theory for doubly connected domains bounded by a sphere and a spheroid', ” Prikl. Mat. Mekh., 24, No. 1, 65–74 (1990).
V. S. Panasyuk, M. M. Stadnik, and V. P. Silovanyuk, Stress Concentration in Three-Dimensional Bodies with Thin Inclusions [in Russian], Naukova Dumka, Kiev (1986).
Yu. N. Podil'chuk, Three-Dimensional Problems of Elastic Theory [in Russian], Naukova Dumka, Kiev (1979).
Yu. N. Podil'chuk and V. S. Kirilyuk, “Shear stress distribution in a circular cylinder with an elastic ellipsoidal inclusion', ” Prikl. Mekh., 22, No. 11, 36–40 (1986).
V. S. Protsenko and A. G. Nikolaev, “Solutions of spatial elastic problems using reexpansion formulas', ” Prikl. Mekh., 22, No. 7, 83–89 (1986).
A. F. Ulitko, The Method of Vector Eigenfunctions in Spatial Elastic Problems [in Russian], Naukova Dumka, Kiev (1979).
H. S. Chen and A. Acrivos, “The solution of the equations of linear elasticity for an infinite region containing two spherical inclusions', ” Int. J. Solid Struct., 14, 349–364 (1978).
R. H. Edwards, “Stress concentration around spheroidal inclusions and cavities', ” J. Appl. Mech., 18, No. 1, 65–73 (1951).
J. D. Eshelby, “The determination of the field of an ellipsoidal inclusion and related problems', ” Proc. Roy. Soc., A 241, 376–396 (1957).
V. S. Kirilyuk, “On a full-strength juncture between an isotropic matrix and an orthotropic inclusion under a triaxial load', ” Int. Appl. Mech., 36, No. 1, 82–89 (2000).
V. I. Kushch, “Elastic equilibrium of a medium containing a finite number of aligned spheroidal inclusions', ” Int. J. Solid Struct., 33, 1175–1189 (1996).
V. I. Kushch, “Elastic equilibrium of a medium containing a finite number of arbitrarily oriented spheroidal inclusions', ” Int. J. Solid Struct., 35, No. 12, 1187–1198 (1998).
Z. A. Moskovidis and T. Mura, “Two ellipsoidal inhomogeneities by the equivalent inclusion method', ” J. Appl. Mech., 42, 847–852 (1975).
T. Mura, Micromechanics of Defects in Solids, Martinus Nijhoff, The Hague, Netherlands (1982).
Yu. N. Podil'chuk and I. V. Lebedeva, “Equilibrium of piezoceramic cylinder with spheroidal cavity', ” Int. Appl. Mech., 35, No. 5, 477–487 (1999).
M. A. Sadowsky and E. Strenberg, “Stress concentration around a triaxial ellipsoidal', ” J. Appl. Mech., 16, No. 2, 149–157 (1949).
J. F. Shelley and Y. Y. Yu, “The effect of two rigid spherical inclusions on the stresses in an infinite elastic solid', ” J. Appl. Mech., 33, 993–998 (1966).
E. Strenberg and M. A. Sadowsky, “On the axisymmetric problem of the theory of elasticity for an infinite region containing two spherical cavities', ” J. Appl. Mech., 19, 19–27 (1952).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kirilyuk, V.S. Interaction of Anisotropic Ellipsoidal Inclusions in an Isotropic Medium under Mechanical Loads and Uniform Heating. International Applied Mechanics 37, 1180–1188 (2001). https://doi.org/10.1023/A:1013286400042
Issue Date:
DOI: https://doi.org/10.1023/A:1013286400042