Abstract
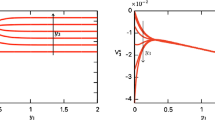
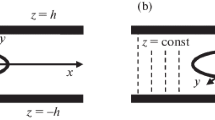
We propose a new procedure for the solution of mixed three-dimensional skew-symmetric problems of the theory of elasticity for a layer weakened by through tunnel cracks. The boundary-value problem is reduced to a system of 3k (k = 1, 2, ...) one-dimensional singular integral equations. We present some results of numerical calculations of the stress intensity factors.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
L. A. Fil'shtinskii, “Periodic solutions of problems of the theory of elasticity and electroelasticity for a cylinder in R 3,” Theor. Appl. Mech., Issue 21, 13–20 (1990).
É. I. Grigolyuk, Yu. D. Kovalev, and L. A. Fil'shtinskii, “Bending of a layer weakened by through tunnel cuts,” Dokl. Akad. Nauk SSSR, 317, No. 1, 51–53 (1991).
V. T. Grinchenko, Equilibrium and Stationary Oscillations of Elastic Bodies of Finite Sizes [in Russian], Naukova Dumka, Kiev (1978).
A. S. Kosmodamianskii and V. A. Shaldyrvan, Thick Multiply Connected Plates [in Russian], Naukova Dumka, Kiev (1978).
A. F. Ulitko, Method of Vector Eigenfunctions in Three-Dimensional Problems of the Theory of Elasticity [in Russian], Naukova Dumka, Kiev (1979).
G. S. Kit and M. V. Khai, Method of Potentials in Three-Dimensional Problems of Thermoelasticity for Cracked Bodies [in Russian], Naukova Dumka, Kiev (1989).
A. E. Andreikiv, Three-Dimensional Problems of the Theory of Cracks [in Russian], Naukova Dumka, Kiev (1982).
S. M. Belotserkovskii and I. K. Lifanov, Numerical Methods in Singular Integral Equations [in Russian], Nauka, Moscow (1985).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Fil'shtinskii, L.A., Kovalev, Y.D. Bending of a Layer with Through Tunnel Cuts and Free-Sliding End Faces. Materials Science 36, 570–574 (2000). https://doi.org/10.1023/A:1011322423868
Issue Date:
DOI: https://doi.org/10.1023/A:1011322423868