Abstract
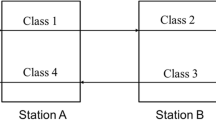
We consider a four-class two-station network with feedback, with fluid inputs and a head-of-the-line generalized processor sharing discipline at each station. We derive the Skorokhod Problem associated with the network and obtain algebraic sufficient conditions for Lipschitz continuity of the associated Skorokhod Map. This provides the first example of a multiclass network with feedback for which the associated Skorokhod Problem has been proved to be regular. As an elementary application, we show that under the conditions which guarantee Lipschitz continuity the network is stable if and only if the usual load conditions apply.
Similar content being viewed by others
References
R. Atar and P. Dupuis, Large deviations and queueing networks: methods for rate function identification, Stochastic Process. Appl. 84 (1999) 255–296.
A. Berman and R.J. Plemmons, Nonnegative Matrices in the Mathematical Sciences (Academic Press, New York, 1979).
A. Bernard and A. El Kharroubi, Regulations de processus dans le premier “orthant” de ℝn, Stochastics 34 (1991) 149–167.
A. Budhiraja and P. Dupuis, Simple necessary and sufficient conditions for the stability of constrained processes, SIAM J. Appl. Math. 59 (1999) 1686–1700.
H. Chen and A. Mandelbaum, Stochastic discrete flow networks: Diffusion approximations and bottlenecks, Ann. Probab. 19 (1991) 1436–1519.
J.G. Dai, On the positive Harris recurrence for multiclass queueing networks: A unified approach via fluid limit models, Ann. Appl. Probab. 5 (1995) 49–77.
P. Dupuis and H. Ishii, On Lipschitz continuity of the solution mapping to the Skorokhod problem with applications, Stochastics 35 (1991) 31–62.
P. Dupuis and A. Nagurney, Dynamical systems and variational inequalities, Ann. Oper. Res. 44 (1993) 9–42.
P. Dupuis and K. Ramanan, A Skorokhod problem formulation and large deviation analysis of a processor sharing model, Queueing Systems 28 (1998) 109–124.
P. Dupuis and K. Ramanan, Convex duality and the Skorokhod problem – I, Probab. Theory Related Fields 115 (1999) 153–195.
P. Dupuis and K. Ramanan, Convex duality and the Skorokhod problem – II, Probab. Theory Related Fields 115 (1999) 197–236.
A. Elwalid and D. Mitra, Design of generalized processor sharing schedulers which statistically multiplex heterogeneous QoS classes, in: Proc. of IEEE INFOCOM 99, 1999.
J.M. Harrison and M.I. Reiman, Reflected Brownian motion on an orthant, Ann. Probab. 9 (1981) 302–308.
V.S. Kozyakin, A. Mandelbaum and A.A. Vladimirov, Absolute stability and dynamic complementarity, Preprint (1993).
P.-L. Lions and A.-S. Sznitman, Stochastic differential equations with reflecting boundary conditions, Comm. Pure Appl. Math. 37 (1984) 511–553.
S.H. Lu and P.R. Kumar, Distributed scheduling based on due dates and buffer priorities, IEEE Trans. Automat. Control 36 (1991) 1406–1416.
K. Majewski, Large deviations of feedforward queueing networks, Ph.D. thesis, Ludwig-Maximilian-Universität München (1996).
A. Mandelbaum, The dynamic complementarity problem, Unpublished manuscript (1989).
A. Mandelbaum and L. Van der Heyden, A characterization of strictly semi-monotone matrices, Unpublished manuscript (1986).
S. Meyn, Transience of multiclass queueing networks via fluid limit models, Ann. Appl. Probab. 5 (1995) 946–957.
W. Peterson, A heavy traffic limit theorem for networks of queues with multiple customer types, Math. Oper. Res. 16 (1991) 90–118.
K. Ramanan and P. Dupuis, Large deviation analysis of data streams that share a buffer, Ann. Appl. Probab. 8 (1998) 1070–1129.
M.I. Reiman, Open queueing networks in heavy traffic, Math. Oper. Res. 9 (1984) 441–458.
M. Reiman and R.J. Williams, A boundary property of semimartingale reflecting Brownian motions, Probab. Theory Related Fields 77 (1988) 87–97.
A.N. Rybko and A.L. Stolyar, Ergodicity of stochastic processes describing the operation of open queueing networks, Problemy Peredachi Informatsii 28 (1992) 3–26.
J. Samuelson, R.M. Thrall and O. Wesler, A partition theorem for Euclidean N-space, Proc. Amer. Math. Soc. 9 (1958) 805–807.
A.F. Veinnot, Jr., Discrete dynamic programming with sensitive discount optimaility criteria, Ann. Math. Statist. 40 (1969) 1635–1660.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Dupuis, P., Ramanan, K. A Multiclass Feedback Queueing Network with a Regular Skorokhod Problem. Queueing Systems 36, 327–349 (2000). https://doi.org/10.1023/A:1011037419624
Issue Date:
DOI: https://doi.org/10.1023/A:1011037419624