Non-linear analysis of geomechanical problems using coupled finite and infinite elements

Abstract

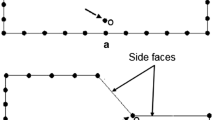
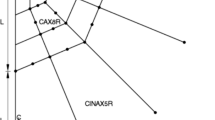
In modeling of many geomechanics problems such as underground openings, soil-foundation structure interaction problems, and in wave propagation problems through semi-infinite soil medium the soil is represented as a region of either infinite or semi-infinite extent. Numerical modeling of such problems using conventional finite elements involves a truncation of the far field in which the infinite boundary is terminated at a finite distance. In these problems, appropriate boundary conditions are introduced to approximate the solution of the infinite or semi-infinite boundaries as closely as possible. However, the task of positioning the finite boundary in conventional finite element discretization and the definition of the boundary and its conditions is very delicate and depends on the modeller's skill and intuition. Moreover, such a choice is influenced by the size of the domain to be discretized. Consequently, the dimensions of the global matrices and the time required for solution of the problem will increase considerably and also selection of the arbitrary location of truncated boundary may lead to erroneous result. In order to over come these problems, mapped infinite elements have been developed by earlier researchers (Simoni and Schrefier, 1987). In the present work the applicability of infinite element technique is examined for different geomechanics problems. A computer program INFEMEP is developed based on the conventional finite element and mapped infinite element technique. It is then validated using selected problems such as strip footing and circular footing. CPU time taken to obtain solutions using finite element approach and infinite element approach was estimated and presented to show the capability of coupled modeling in improving the computational efficiency. Mesh configurations of different sizes were used to explore the enhancement of both computational economy and solution accuracy achieved by incorporation of infinite elements to solve elastic and elasto-plastic problems in semi-infinite/finite domain as applied to geotechnical engineering. © Rapid Science Ltd. 1998