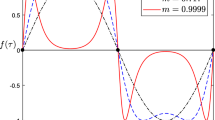
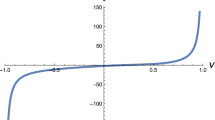
Abstract
A study is made of the dynamics of oscillating systems with a slowly varying parameter. A slowly varying forcing periodically crosses a critical value corresponding to a pitchfork bifurcation. The instantaneous phase portrait exhibits a centre when the forcing does not exceed the critical value, and a saddle and two centres with an associated double homoclinic loop separatrix beyond this value. The aim of this study is to construct a Poincaré map in order to describe the dynamics of the system as it repeatedly crosses the bifurcation point. For that purpose averaging methods and asymptotic matching techniques connecting local solutions are applied. Given the initial state and the values of the parameters the properties of the Poincaré map can be studied. Both sensitive dependence on initial conditions and (quasi) periodicity are observed. Moreover, Lyapunov exponents are computed. The asymptotic expressions for the Poincaré map are compared with numerical solutions of the full system that includes small damping.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Guckenheimer, J. and Holmes, P., Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer-Verlag, New York, 1983.
Its, A. R., Fokas, A. S., and Kapaev, A. A., ‘On the asymptotic analysis of the Painlev00E9 equations via the isomonodromy method’, Nonlinearity 7, 1994, 1291–1325.
Lichtenberg, A. J. and Lieberman, M. A., Regular and Stochastic Motion, Springer-Verlag, Berlin, 1983.
Bridge, J. and Rand, R. H., ‘Chaos and symbol sequences in systems with a periodically disappearing figureeight separatrix’, in Proceedings of 1992 ASME Bifurcation Phenomena and Chaos in Thermal Convection, Vol. 214, 1992, pp. 47–55.
Coppola, V. T. and Rand, R. H., ‘Computer algebra, elliptic functions and chaos’, in Proceedings of 1990 ASME International Computers in Engineering Conference, Vol. 1, Boston, MA, August 6–10, 1990, pp. 193–200.
Coppola, V. T. and Rand, R. H., ‘Chaos in a system with a periodically disappearing separatrix’, Nonlinear Dynamics 1, 1990, 401–420.
Eckhaus, W., Asymptotic Analysis of Singular Perturbations, North-Holland, Amsterdam/New York/Oxford, 1979.
Verhulst, F., Nonlinear Differential Equations and Dynamical Systems, Springer-Verlag, Berlin, 1990.
Sanders, J. A. and Verhulst, F., Averaging Methods in Nonlinear Dynamical Systems, Springer-Verlag, New York, 1985.
Bourland, F. J. and Haberman, R., ‘separatrix crossing: Time-invariant potentials with dissipation’, SIAM Journal of Applied Mathematics 50, 1990, 1716–1744.
Neihstadt, A. I., ‘Passage through a separatrix in a resonance problem with a slowly-varying parameter’, Journal of Applied Mathematics and Mechanics (PMM) 39, 1975, 594–605.
Bosley, D. L. and Kevorkian, J., ‘sustained resonance in very slowly varying oscillatory Hamiltonian systems’, SIAM Journal of Applied Mathematics 52, 1992, 494–527.
Marée, G. J. M., ‘sudden change in a second-order non-linear system with a slowly varying parameter’, International Journal of Non-Linear Mechanics 28, 1993, 409–426.
Kaper, T. J. and Wiggins, S., ‘Lobe area in adiabatic Hamiltonian systems’, Physica D 51, 1991, 205–212.
Haberman, R., ‘slowly varying jump and transition phenomena associated with algebraic bifurcation problems’, SIAM Journal of Applied Mathematics 37, 1979, 69–106.
Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions, National Bureau of Standards, Washington, DC, 1964.
Marée, G. J. M., ‘slow passage through a pitchfork bifurcation’, SIAM Journal of Applied Mathematics 56, 1996, 889–918.
Ott, E., Chaotic Dynamics, Cambridge University Press, Cambridge, 1993.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Maree, G.J.M. Slow Periodic Crossing of a Pitchfork Bifurcation in an Oscillating System. Nonlinear Dynamics 12, 1–37 (1997). https://doi.org/10.1023/A:1008247430863
Issue Date:
DOI: https://doi.org/10.1023/A:1008247430863