Skip to main content
SpringerLink
Log in

Spacing of edge fractures in layered materials

  • Published:
International Journal of Fracture Aims and scope Submit manuscript

Abstract

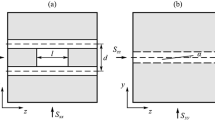
Opening-mode fractures developed from a free surface in a layered material often terminate at the interface that divides the fractured layer and the underlying layer. They also display regular spacing that is of the same order of magnitude as the thickness of the fractured layer. We have investigated the stress distribution between two adjacent edge fractures as a function of the ratio of fracture spacing to thickness of the fractured layer using a two-layer elastic model with a fractured top layer. The results show that when the ratio of fracture spacing to the layer thickness changes from greater than to less than a critical value the normal stress acting perpendicular to the fractures near the free surface changes from tensile to compressive. This stress state transition precludes further infilling of fractures unless they are driven by mechanisms other than a pure extension, or there are flaws that significantly perturb the local stress field between the fractures. Hence, the critical fracture spacing to layer thickness ratio defines a lower limit for fractures driven by extension, which also defines the condition of fracture saturation. The critical value of the fracture spacing to layer thickness ratio is independent of the average strain of the fractured layer, and it increases with increasing ratio of Young's modulus of the fractured layer to that of the underlying layer. The critical value increases with increasing Poisson's ratio of the fractured layer, but it decreases with increasing Poisson's ratio of the underlying layer. For the case with the same elastic constants for the fractured layer and the underlying layer, the critical spacing to layer thickness ratio is about 3.1. Delamination between the fractured layer and the underlying layer makes the critical spacing to layer thickness ratio much greater. Infilling fractures grow more easily from flaws located near the bottom of the fractured layer than from those located near the free surface when the spacing to layer thickness ratio is less than the critical value. The propagation of an edge flaw between adjacent edge fractures is unstable, but for the flaw to propagate to the interface, its height has to be greater than a critical size, that decreases with increasing fracture spacing to layer thickness ratio. The propagation behavior of an internal flaw with its lower tip at the interface depends on the edge fracture spacing to layer thickness ratio. The propagation is unstable, when the fracture spacing to layer thickness ratio is greater than a critical value; stable, when the fracture spacing to layer thickness ratio is less than another critical value; and first unstable, then stable, and/or unstable again, when the fracture spacing to layer thickness ratio is between these two critical values.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Aveston, J., Cooper, G.A. and Kelly, A. (1971). The Properties of Fiber Composites, IPC Sci. Technol. Press.

  • Bai, T. and Pollard, D.D. (2000). Fracture spacing in layered rocks: a new explanation based on the stress transition. Journal of Structural Geology 22, 43–57.

    Google Scholar 

  • Barber, J.R. (1992). (edited by Gladwell, G.M.L.) Solid Mechanics and its Applications In: Elasticity (Volume 12), Kluwer Academic Publishers, London, 293 pp.

    Google Scholar 

  • Barsoum, R.S. (1976). On the use of isoparametric finite elements in linear fracture mechanics. International Journal of Num. Meth. Eng. 10, 25–37.

    Google Scholar 

  • Bazant, Z.P., Ohtsubo, H. and Aoh, K. (1979). Stability and post-critical growth of a system of cooling and shrinkage cracks, Int. J. Fracture 15, 443–456.

    Google Scholar 

  • Bittencourt, T.N., Barry, A. and Ingraffea, A.R. (1992). Comparison of Mixed-Mode Stress-Intensity Factor Obtained Through Displacement Correlation, J-integral Formulation, and Modified Crack-Closure Integral In: Fracture Mechanics (edited by Atluri, S.N., Newman, J.C. Jr., Raju, I.S. and Epstein, J.S.), Twenty-Second Symposium (vol. II), ASTMSTP 1131, American Society for Testing and Materials, Philadelphia, pp. 69–82.

    Google Scholar 

  • Bittencourt, T.N., Wawrzynek, P.A., Ingraffea, A.R. and Sousa, J.L. (1996). Quasi-automatic simulation of crack propagation for 2D LEFM problems. Engineering Fracture Mechanics 55, 321–334.

    Google Scholar 

  • Cherepanov, G.P. (1994). On the theory of thermal stresses in a thin film on a ceramic substrate, Journal of Applied Physics 75, 844–849.

    Google Scholar 

  • Degraff, J.M. and Aydin, A. (1993). Effect of thermal regime on growth increment and spacing of contraction joints in basaltic lava. Journal of Geophysical Research 98, 6411–6430.

    Google Scholar 

  • Drory, M.D., Thouless, M.D. and Evans, A.G. (1988). On the decohesion of residually stressed thin films. Acta Metall. 36, 2019–2028.

    Google Scholar 

  • Drozdov, A.D. (1998). Mechanics of Viscoelastic Solids, Wiley, New York, 472 pp.

    Google Scholar 

  • Dundurs, J. (1969). Discussion on edge bonded dissimilar orthogonal elastic wedges under normal and shear loading. ASME Journal of Applied Mechanics 36, 650–652.

    Google Scholar 

  • Fischer, M.P., Gross, M.R., Engelder, T. and Greenfield, R.J. (1995). Finite-element analysis of the stress distribution around a pressurized crack in a layered elastic medium: implications for the spacing of fluid-driven joints in bedded sedimentary rock. Tectonophysics 247, 49–64.

    Google Scholar 

  • Garino, T.J. and Bowen, H.K. (1987). Deposition and sintering of particle films on a rigid substrate, Journal of American Ceramics Society 70, C315–317. 394

    Google Scholar 

  • Garrett, K.W. and Bailey, J.E. (1977a). Multiple transverse fracture in 90E cross-ply laminates of a glass fibrereinforced polyester. Journal of Materials Science. 12, 157–168.

    Google Scholar 

  • Garrett, K.W. and Bailey, J.E. (1977b). The effect of resin failure strain on the tensile properties of glass fibrereinforced polyester cross-ply laminates. Journal of Materials Science 12, 2189–2194.

    Google Scholar 

  • Griffith, A.A. (1921). The phenomena of rupture and flow in solids. Philosophy Transactions Royal Society London, A 221, 163–198.

    Google Scholar 

  • Gross, M.R. (1993). The origin and spacing of cross joints: examples from Monterey Formation, Santa Barbara Coastline, California. Journal of Structural Geology 15, 737–751.

    Google Scholar 

  • Gross, M.R., Fischer, M.P., Engelder, T. and Greenfield, R.J. (1995). Factors controlling joint spacing in interbedded sedimentary rocks: integrating numerical models with field observations from the Monterey Formation, USA. In: Fractography: Fracture Topography as a Tool in Fracture Mechanics and Stress Analysis (edited by Ameen, M.S.) Geological Society Special Publication No. 92, pp. 215–233.

  • He, M.Y. and Hutchinson, J.W. (1989). Kinking of a crack out of an interface. Journal of Applied Mechanics 56, 270–278.

    Google Scholar 

  • Henshall, R.D. and Shaw, K.G. (1975). Crack tip elements are unnecessary. International Journal of Numerical Methods Engineering 9, 495–509.

    Google Scholar 

  • Hobbs, D.W. (1967). The formation of tension joints in sedimentary rocks: an explanation. Geological Magazine 104, 550–556.

    Google Scholar 

  • Hong, A.P., Li, Y.N. and Bazant, P. (1997). Theory of crack spacing in concrete pavements. Journal of Engineering Mechanics 123, 267–275.

    Google Scholar 

  • Hu, M.S. and Evans, A.G. (1989). The cracking and decohesion of thin films on ductile substrates. Acta Metall. 37, 917–925.

    Google Scholar 

  • Hu, M.S., Thouless, M.D. and Evans, A.G. (1988). Decohesion of thin films from brittle substrates. Acta Metall., 36, 1301–1307.

    Google Scholar 

  • Hughes, T.J.R. (1987). The Finite Element Method, Prentice-HallEnglewood Cliffs, New Jersey, 803 pp.

    Google Scholar 

  • Ingraffea, A.R. (1990). Case studies of simulation of fracture in concrete dams. Fracture Mechanics 35, 553–564.

    Google Scholar 

  • Irwin, G.R. (1948). Fracture dynamics. In: Fracturing of Metals, Am. Soc. Metals, Cleveland, Ohio.

    Google Scholar 

  • Lawn, B.R. and Wilshaw, T.R. (1975). Fracture of Brittle Solids, Cambridge University Press, Cambridge.

    Google Scholar 

  • Kemeny, J. and Cook, N.G.W. (1985). Formation and stability of steeply dipping joint sets. In: Research and Engineering Applications in Rock Masses (edited by Ashworth, E.) Proceedings of the 26th U.S. Symposium on Rock Mechanics, 26, pp. 471–478.

  • Konrad, J.-M. and Shen, M. (1997). Prediction of the spacing between thermal contraction cracks in asphalt pavements. Canadian Journal of Civ. Eng. 24, 288–302.

    Google Scholar 

  • Lachenbruch, A.H. (1961). Depth and spacing of tension cracks. Journal of Geophysical Research 66, 4273–4292.

    Google Scholar 

  • Lachenbruch, A.H. (1962). Mechanics of thermal contraction cracks and ice- wedge polygons in permafrost. Geological Society of America Special Paper 70, 69.

    Google Scholar 

  • Linsbauer, H.N., Ingreffea, A.R., Rossmanith, H.P. and Wawrzynek, P.A. (1989). Simulation of cracking in large arch dam: Part I, J. Struct. Engng. 115, 1599–1615.

    Google Scholar 

  • Nemat-Nasser, S., Sumi, Y. and Keer, L.M. (1980). Unstable growth of tension cracks in brittle solids: stable and unstable bifurcations, snap-through, and imperfection sensitivity. International Journal of Solids Structures 16, 1017–1035.

    Google Scholar 

  • Nur, A. (1982). The origin of tensile fracture lineaments Journal of Structural Geology 4, 31–40.

    Google Scholar 

  • Ochiai, S. and Hojo, M. (1995). Multiple cracking of a coating layer and its influence on fibre strength. Journal of Material Science 30, 274–279.

    Google Scholar 

  • Orowan, E. (1950). Fundamentals of brittle behavior in metals. In: MIT Symposium on Fatigue and Fracture of Metals, John Wiley and Sons, New York.

    Google Scholar 

  • Parvizi, A. and Bailey, J.E. (1978). On multiple transverse cracking in glass fibre epoxy cross-ply laminates. Journal of Materials Science 13, 2131–2136.

    Google Scholar 

  • Pollard, D.D. and Aydin, A. (1988). Progress in understanding jointing over the past century. Geological Society of America Bulletin 100, 1181–1204.

    Google Scholar 

  • Pollard, D.D. and Holzhausen, G. (1979). On the mechanical interaction between a fluid-filled fracture and the earth surface. Tectonophysics 53, 27–57.

    Google Scholar 

  • Pollard, D.D. and Segall, P. (1987). Theoretical Displacements and Stresses near Fractures in Rocks: with Applications to Faults, Joints, Veins, Dikes and Solution Surfaces. In: Fracture Mechanics of Rock (edited by Atkinson, B.K.) Academic Press, London, pp. 277–349.

    Google Scholar 

  • Raju, I.S. (1987). Calculation of strain-energy release rates with higher order and singular elements, Engineering of Fracture Mechanics 28, 251–274.

    Google Scholar 

  • Reiter, M., Barroll, M.W., Minier, J. and Clarkson, G. (1987). Thermo-mechanical model for incremental fracturing in cooling lava flows. Tectonophysics 142, 241–260.

    Google Scholar 

  • Rice, J.R. and Rosengren, G.F. (1968). Plane-strain deformation near a crack for a power-law hardening material. Journal of Mechenical Physics of Solids. 16, pp1–12.

    Google Scholar 

  • Rives, T. and Petit, J.-P. (1990). Experimental Study of Jointing Cylindrical and Non-Cylindrical folding In: Mechanics of Jointed and Faulted Rock (edited by Rossmanith), Balkema, Rotterdam.

  • Rives, T., Rawnsley, K.D. and Petit, J.-P. (1994). Analogue simulation of natural orthogonal joint set formation in brittle varnish. Journal of Structural Geology 16, 419–429.

    Google Scholar 

  • Rybicki, E.F. and Kanninen, M.F. (1977). A finite element calculation of stress intensity factors by modified crack closure integral. Engineering Fracture Mech. 9, 931–938.

    Google Scholar 

  • Shih, C.F., de Lorenzi, H.G. and German, M.D. (1976). Crack extension modelling with singular quadratic isoparametric elements. International Journal of Fracture 12, 647–651.

    Google Scholar 

  • Tada, H., Paris, P.C. and Irwin, G.R. (1985). The Stress Analysis of Cracks Handbook, 2nd ed., Paris Productions Incorporated and Del Research Corporation, St. Louis, Missouri.

    Google Scholar 

  • Thouless, M.D. (1989). Some mechanics for the adhesion of thin films. Thin Solid Films 181, 397–406.

    Google Scholar 

  • Thouless, M.D. (1990). Crack spacing in brittle films on elastic substrates. Journal of American Ceramic Society 73, 2144–2146.

    Google Scholar 

  • Thouless, M.D., Olsson, E. and Gupta, A. (1992). Cracking of brittle films on elastic substrates. Acta Metall. Mater. 40, 1287–1292.

    Google Scholar 

  • Tracey, D.M. (1971). Finite elements for determination of crack tip elastic stress intensity factors. Engng. Fracture Mech. 3, 255–256.

    Google Scholar 

  • Tracey, D.M. (1977). Discussion of 'On the use of isoparametric finite elements in linear fracture mechanics'. Int. J. Num. Meth. Engng 11, 401–402.

    Google Scholar 

  • Watkins, T.R. and Green, D.J. (1993). Fracture behavior of chemically-vapor-deposited SiC-coated graphite: I experimental results. J. Am. Ceram. Soc. 76, 3066–3072.

    Google Scholar 

  • Wawrzynek, P.A. and Ingraffea, A.R. (1987). Interactive finite element analysis of fracture processes: An integrated approach. Theoretical and Applied Fracture Mechanics 8, 137–150.

    Google Scholar 

  • Wu, H. (1995). A model study of fracture generation in layered brittle rocks with applications to predicting subsurface fracture networks, Ph.D. Thesis, Stanford University, Stanford, California, 175 pp.

    Google Scholar 

  • Wu, H.-C. and Li, V.C. (1992). Snubbing and bundling effects on multiple crack spacing of discontinuous random fiber-reinforced brittle matrix composites. J. Am. Ceram. Soc. 75, 3487–3489.

    Google Scholar 

  • Wu, H. and Pollard, D.D. (1992). Propagation of a set of opening-mode fractures in layered brittle materials under uniaxial strain cycling. Journal of Geophysical Research, B, Solid Earth and Planets 97, 3381–3396.

    Google Scholar 

  • Wu, H. and Pollard, D.D. (1995). An experimental study of the relationship between joint spacing and layer thickness. Journal of Structural Geology 17, 887–905.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Geological and Environmental Sciences, Stanford University, Stanford, CA, 94305-2115, USA

    Taixu Bai & David D. Pollard

  2. Department of Mechanical Engineering, Stanford University, Stanford, CA, 94305-4040, USA

    Huajian Gao

Authors
  1. Taixu Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David D. Pollard
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huajian Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bai, T., Pollard, D.D. & Gao, H. Spacing of edge fractures in layered materials. International Journal of Fracture 103, 373–395 (2000). https://doi.org/10.1023/A:1007659406011

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1007659406011

Search

Navigation