Abstract
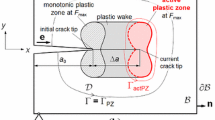
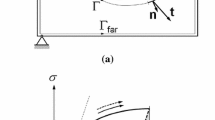
The J-integral is applied to a Dugdale crack perpendicular to an interface of materials with equal elastic properties but different yield stresses. It is shown that the integral is path independend with certain limitations to the integration path. Three essentially different paths can be distinguished. The first integration path is totally within the first material, it provides the local crack driving force. Performing the integral around the plastic zone in both materials gives the global crack driving force. An interface force can be defined by evaluating the integral along both sides of the plastically deformed region of the interface. A comparison of these three integrals reveals that the global crack driving force is equal to the sum of the local crack driving force and of the interface force. The derived expression for the J-integral are compared with the crack tip opening displacement published recently. This reveals that the local J describes the plastic deformation at the crack tip. Therefore it represents the crack driving force in bimaterials as it does the conventional J-integral in case of homogeneous materials. The analyses are also extended to cyclic plasticity, where an out-of-phase effect is observed. Finally it is discussed how these results can be used to explain fatigue tests at bimaterial specimens.
Similar content being viewed by others
References
Anderson, T.L. (1995). Fracture Mechanics. Fundamentals and Applications., CRC Press, Florida.
Barenblatt, G.I. (1962). The mathematical theory of equilibrium cracks in brittle solids. Advances Applied Mechanics 7, 55–129.
Bilby, B.A., Cottrell, A.H. and Swinden, K.H. (1963). The spread of yielding from a notch. Proceedings Royal Society of London A272, 304–314.
Cook, T.S. and Erdogan, F. (1972). Stresses in bonded materials with a crack perpendicular to the interface. International Journal of Engineering Science 10, 677–697.
Dowling, N.E. and Begley, J.A. (1976). Fatigue crack growth during gross plasticity and the J - integral. ASTM STP 590, 82–103.
Dugdale, D.S. (1960). Yielding of steel sheets containing slits. Journal of Mechanics Physics and Solids 8, 100–108.
England A.H.: (1965). A crack between dissimilar media. Journal of Applied Mechanics 32, 400–401.
Erdogan, F. and Biricikoglu, V. (1973). Two bonded half-planes with a crack going through the interface. International Journal of Engineering Science 11, 745–766.
Eshelby, J.O. (1956). The continuum theory of lattice defects. Solar State Physics 3, 79–144.
Kim, A.S., Suresh, S. and Shih, C.F. (1997). Plasticity effects on fracture normal to interfaces with homogeneous and graded compositions. International Journal of Solids and Structures 34, 3415–3432.
Newman, Jr. J.C. (1981). A crack closure model for predicting fatigue crack growth under random loading. Mechanics of Fatigue Crack Closure ASTM STP 768, 53–84.
Pippan, R. and Riemelmoser, F.O. (1998). Fatigue of bimaterials. Investigation of the plastic mismatch in case of cracks perpendicular to the interface. Computational Materials Science 13, 108–116.
Pippan, R., Flechsig, K. and Riemelmoser, F.O. (1999). Fatigue crack propagation behaviour in the vicinity of an interface between materials with different yield stresses. Materials Science Engineering (in press).
Rice, J.R. (1967). Mechanics of crack tip deformation and extension by fatigue. ASTM STP 415, 247–309.
Rice, J.R. (1968), A path independent integral and approximate analysis of strain concentrations by notches and cracks. Journal of Applied Mechanics 35, 379–386.
Riemelmoser, F.O. and Pippan, R. (1998). An inclined strip yield model for describing monotonic and cyclic plasticity. Proceedings ICES98. 2, 1456–1461.
Sugimura, Y., Lim, P.G., Shih, C.F. and Suresh, S. (1995). Fracture normal to a bimaterial interface effects of plasticity on crack-tip shielding and amplification. Acta Metallurgica et Materialia 43, 1157–1169.
Suresh S., Sugimura Y. and Tschegg E.K. (1992). The growth of a fatigue-crack approaching a perpendicularlyoriented, bimaterial interface. Scripta Metallurgica et Materialia 27, 1189–1194.
Tada, H., Paris, P.C. and Irwin, G.R. (1985). Del Research Corporation, St. Louis, Missouri. The stress analysis of cracks handbook.
Wappling, D., Gunnars, J. and Stahle, P. (1998). Crack growth across a strength mismatched bimaterial interface. International Journal of Fracture 89, 223–243.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Riemelmoser, F.O., Pippan, R. The J-integral at Dugdale cracks perpendicular to interfaces of materials with dissimilar yield stresses. International Journal of Fracture 103, 397–418 (2000). https://doi.org/10.1023/A:1007605224764
Issue Date:
DOI: https://doi.org/10.1023/A:1007605224764