Abstract
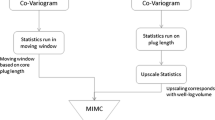
When seismic data and porosity well logs contain information at different spatial scales, it is important to do a scale-matching of the datasets. Combining different data types with scale mismatch can lead to suboptimal results. A good correlation between seismic velocity and rock properties provides a basis for integrating seismic data in the estimation of petrophysical properties. Three-dimensional seismic data provides an unique exhaustive coverage of the interwell reservoir region not available from well data. However, because of the limitations of measurement frequency bandwidth and view angles, the seismic image can not capture the true seismic velocity at all spatial scales present in the earth. The small-scale spatial structure of heterogeneities may be absent in the measured seismic data. In order to take best advantage of the seismic data, factorial kriging is applied to separate the small and large-scale structures of both porosity and seismic data. Then the spatial structures in seismic data which are poorly correlated with porosity are filtered out prior to integrating seismic data into porosity estimation.
Similar content being viewed by others
REFERENCES
Bourgault, G., 1994, Robustness of noise filtering by kriging analysis: Math. Geology, v. 26, no. 6, p. 733–752.
Chu, J., 1993, Conditional fractal simulation, sequential indicator simulation and interactive variogram modeling: unpublished PhD dissertation, Stanford University, Stanford, CA.
Deutsch, C. V., and Journel, A. G., 1996, GSLIB: Geostatistical software library and user's guide, 2nd Ed.: Oxford University Press, New York, 340 p.
Devaney, A. J., 1984, Geophysical diffraction tomography: IEEE Trans. Geo. Remote Sense, GE-22, no. 1, p. 3–13.
Gómez-Hernández, J. J., 1991, A stochastic approach to the simulation of block conductivity fields conditioned upon data measured at a smaller scale: unpublished PhD dissertation, Stanford University, Stanford, CA, 351 p.
Goovaerts, P., 1992, Factorial kriging analysis: A useful tool for exploring the structure of multivariate spatial information: J. Soil Sci., v. 43, no. 4, p. 597–619.
Goovaerts, P., 1997, Geostatistics for natural resources evaluation: Oxford Univ. Press, New York, 483 p.
Goovaerts, P., and Webster, R., 1994, Scale-dependent correlation between topsoil copper and cobalt concentrations in Scotland: Eur. J. Soil Sci., v. 45, no. 1, p. 79–95.
Goovaerts, P., Sonnet, P., and Navarre, A., 1993, Factorial kriging analysis of spring-water contents in the Dyle river basin, Belgium: Water Resources Res., v. 29, no. 7, p. 2115–2125.
Han, D.-H., 1986, Effects of porosity and clay content on acoustic properties of sand stones and unconsolidated sediments: unpublished doctoral dissertation, Stanford University, Stanford, CA, 210 p.
Harris, J. M., 1987, Diffraction tomography with arrays of discrete sources and receivers: IEEE Trans. Geosci. Remote Sensing, GE-25, no. 4, p. 448–455.
Huang, X., and Kelkar, M., 1996, Integration of dynamic data for reservoir characterization in the frequency domain: Paper SPE 36513 presented at the 1996 SPE Annual Tech. Conf. and Exhib., Denver, Colorado, USA.
Isaaks, E. H., and Srivastava, R. M., 1988, Spatial continuity measures for probabilistic and deterministic geostatistics: Math. Geology, v. 20, no. 4, p. 313–341.
Jaquet, O., 1989, Factorial kriging analysis applied to geological data from petroleum exploration: Math. Geology, v. 21, no. 7, p. 683–691.
Journel, A. G., and Huijbregts, Ch., J., 1978, Mining Geostatistics: Academic Press, New York, 600 p.
Ma, Y. Z., and Myers, D. E., 1994, Simple and ordinary factorial cokriging, in Fabbri, A. G., and Royer, G. G., eds., 3rd CODATA Geomathematics and Geostatistics Conference: Science de la terre, Ser. Inf., Nancy, v. 32, p. 49–62.
Ma, Y. Z., and Royer, J. J., 1988, Local geostatistical filtering application to remote sensing: Sci de la terre, Ser. Informat. Geologique, v. 27, part 1, p. 985–986.
Mavko, G. M., and Burg, J. P., 1987, Two-dimensional maximum entropy spectral analysis, Expanded Abstr., 57th Annual International Meeting, Society of Exploration Geophysicists, p. 603–606.
Mukerji, T., Mavko, G., and Rio, P., 1997, Scales of reservoir heterogeneities and impact of seismic resolution on geostatistical integration, Math. Geology, v. 29, no. 7, p. 933–950.
Sandjivy, L., 1984, The factorial kriging analysis of regionalized data. Its application to geochemical prospecting, in Verly, G., and others, eds., Geostatistics for natural resource characterization: Reidel, Dordrecht, Holland, p. 559–572.
Sandjivy, L., and Galli, A., 1984, Analyse krigeante et analyse spectrale: Sci. de la terre, Ser. Informat. Geologique, v. 21, p. 115–124.
Tran, T. T., 1995, Stochastic simulation of permeability fields and their scale-up for flow modeling: unpublished doctoral dissertation, Stanford University, Stanford, CA, 237 p.
Wackernagel, H., 1988, Geostatistical Techniques for Interpreting Multivariate Spatial Information, in Chung, C., Fabbri, A. G., and Sinding-Larsen, R., eds., Quantitative analysis of mineral and energy resources: Reidel, Dordrecht, Holland, p. 738.
Wen, R., and Sinding-Larsen, R., 1997, Image filtering by factorial kriging-sensitivity analysis and application to Gloria side-scan sonar images: Math. Geology, v. 29, no. 4, p. 433–468.
Wu, R., and Töksoz, M. N., 1987, Diffraction tomography and multisource holography applied to seismic imaging: Geophysics, v. 52, no. 1, p. 11–25.
Yao, T., and Mukerji, T., 1996, Application of factorial kriging to improve seismic data integration, in Baffi, E. Y., and Schofield, N. A., eds., Geostatistics Wollongong' 96: p. 350–361.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Yao, T., Mukerji, T., Journel, A. et al. Scale Matching with Factorial Kriging for Improved Porosity Estimation from Seismic Data. Mathematical Geology 31, 23–46 (1999). https://doi.org/10.1023/A:1007589213368
Issue Date:
DOI: https://doi.org/10.1023/A:1007589213368