Skip to main content
SpringerLink
Log in

Singularity Analysis and Boundary Integral Equation Method for Frictional Crack Problems in Two-Dimensional Elasticity

  • Published:
International Journal of Fracture Aims and scope Submit manuscript

Abstract

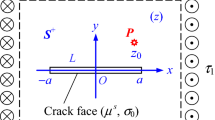
This study investigates the stress singularities in the neighborhood of the tip of a sliding crack with Coulomb-type frictional contact surfaces, and applies the boundary integral equation method to solve some frictional crack problems in plane elasticity. A universal approach to the determination of the complex order of stress singularity is established analytically by using the series expansion of the complex stress functions. When the cracks are open, or when no friction exists between the upper and lower crack faces, our results agree with those given by Williams. When displacement and traction are prescribed on the upper and lower crack surfaces (or vice versa), our result agrees with those by Muskhelishvili. For the case of a closed crack with frictional contact, the only nonzero stress intensity factor is that for pure shear or sliding mode. By using the boundary integral equation method, we derive analytically that the stress intensity factor due to the interaction of two colinear frictional cracks under far field biaxial compression can be expressed in terms of E(k) and K(k) (the complete elliptic integrals of the first and second kinds), where k=[1-(a/b)2]1/2 with 2a the distance between the two inner crack tips and b- a the length of the cracks. For the case of an infinite periodic colinear crack array under remote biaxial compression, the mode II stress intensity factor is found to be proportional to [2b tan(π a/2b)]1/2 where 2a and 2b are the crack length and period of the crack array.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abramowitz, M. and Stegun, I.A. (1964). Handbook of Mathematical Functions. Dover, New York.

    MATH  Google Scholar 

  • Ashby, M.F. and Hallam, S.D. (1986). The failure of brittle solids containing small cracks under compressive stress states. Acta Metallurgy 34, 3497–510.

    Google Scholar 

  • Bogy, D.B. (1968). Edge-bonded dissimilar orthogonal elastic wedge under normal and shear loading. ASME Journal of Applied Mechanics 35, 460–466.

    MATH  Google Scholar 

  • Carpenter, W.C. (1984). A collocation procedure for determining fracture mechanics parameters at a corner. International Journal of Fracture 24, 255–266.

    Article  Google Scholar 

  • Chau, K.T. and Wang, Y.B. (1998). A new boundary integral formulation for two-dimensional elastic bodies containing cracks and holes. International Journal of Solids and Structures (accepted, in press).

  • Chou, S.I. (1997). Stress field around holes in antiplane shear using complex variable boundary element method. Journal of Applied Mechanics 64, 432–435.

    MATH  Google Scholar 

  • Comninou, M. (1977). Interface cracks with friction in the contact zone. Journal of Applied Mechanics, ASME 44, 780–781.

    Google Scholar 

  • Dempsey, J.P. (1959). Power-logarithmic stress singularities at bi-material corners and interface cracks. Journal of Adhesion Science Technology 9, 253–265.

    Google Scholar 

  • Deng, X. (1994a). An asymptotic analysis of stationary and moving cracks with frictional contact along bimaterial interfaces and in homogeneous solids. International Journal of Solids and Structures 31, 2407–2429.

    Article  MATH  Google Scholar 

  • Deng, X. (1994b). A note on interface cracks with and without friction in contact zone. Journal of Applied Mechanics, ASME 61, 994–995.

    Article  MATH  Google Scholar 

  • England, A.H. (1971). On the stress singularities in linear elasticity. International Journal of Engineering Science 9, 571–585.

    Article  MATH  Google Scholar 

  • Fond, C. and Berthaud, Y. (1995). Extensions of the pseudo tractions technique for friction in cracks, circular cavities and external boundaries; effect of the interactions on the homogenised stiffness. International Journal of Fracture 74, 1–28.

    Article  Google Scholar 

  • Gradshteyn, I.S. and Ryzhik, I.M. (1994). Table of Integrals, Series, and Products. Academic Press, Inc., Boston.

    MATH  Google Scholar 

  • Hao, T.H. and Zhu, W. (1993). Collinear periodic cracks in anisotropic viscoelastic plane with surface separation and friction sliding. Engineering Fracture Mechanics 44, 217–229.

    Article  Google Scholar 

  • Hein, V.L. and Erdogan, F. (1971). Stress singularities in a two-material wedge. International Journal of Fracture Mechanics 7, 317–330.

    Article  Google Scholar 

  • Hong, C.C. and Stern, M. (1978). The comparison of stress intensity factors in dissimilar material. Journal of Elasticity 8, 21–34.

    Article  MATH  Google Scholar 

  • Horii, H. and Nemat-Nasser, S. (1985). Compression-induced microcrack growth in brittle solids: axial splitting and shear failure. Journal of Geophysical Research 90, 3105–3125.

    Article  ADS  Google Scholar 

  • Hromadka II, T.V. and Lai, C. (1986). The Complex Variable Boundary Element Method in Engineering Analysis. Springer-Verlag, New York.

    Google Scholar 

  • Irwin, G.R. (1957). Analysis of stresses and strains near the end of a crack traversing a plate. Journal of Applied Mechanics 24, 361–364.

    Google Scholar 

  • Kranz, R.L. (1979). Crack-crack and crack-pore interactions in stressed granite. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstract 16, 37–47.

    Article  Google Scholar 

  • Lazzarin, P. and Tovo, R. (1996). A unified approach to the evaluation of linear elastic stress fields in the neighborhood of cracks and notches. International Journal of Fracture 78, 3–19.

    Article  Google Scholar 

  • Linkov, A.M. and Mogilevskaya, S.G. (1990). Hypersingular integrals in plane problems of the theory of elasticity. Journal of Applied Mathematics and Mechanics (PMM) 54, 93–99.

    Article  MATH  MathSciNet  Google Scholar 

  • Linkov, A.M. and Mogilevskaya, S.G. (1994). Complex hypersingular integrals and integral equations in plane elasticity. Acta Mechanica 105, 189–205.

    Article  MATH  MathSciNet  Google Scholar 

  • Linkov, A.M., Mogilevskaya, S.G. and Napier, J.A.L. (1977). Multiple interacting curvilinear crack problems: A method of solution and numerical results. International Journal of Rock Mechanics and Mining Science 34, Paper No. 218.

    Google Scholar 

  • Liu, J.B., Sharan, S.K., Wang, D. and Yao, L. (1995). A dynamic contact force model for contactable cracks with static and kinetic friction. Computer Methods in Applied Mechanics and Engineering 123, 287–298.

    Article  Google Scholar 

  • Lyuksyutov, I.F. (1995). Dynamical friction and instability of interface motion. Journal of Physics: Condensed Matter 7, 7153–7161.

    Article  ADS  Google Scholar 

  • Muhlhaus, H.B., Chau, K.T. and Ord, A. (1996). Bifurcation of crack pattern in arrays of two-dimensional cracks. International Journal of Fracture 77, 1–14.

    Article  Google Scholar 

  • Muskhelishvili, N.I. (1975). Some Basic Problems of the Mathematical Theory of Elasticity. Noordhoff International, Leyden, Netherlands.

    MATH  Google Scholar 

  • Muskhelishvili, N.I. (1977). Singular Integral Equations. Noordhoff International, Leyden, Netherlands.

    Google Scholar 

  • Nakanishi, N. (1994). Continuum model of mode-III crack propagation with surface friction. Physical Review E 49, 5412–5419.

    Article  ADS  Google Scholar 

  • Nemat-Nasser, S. and Obata, M. (1988). A microcrack model of dilatancy in brittle material. Journal Applied Mechanics ASME 55, 24–35.

    Article  Google Scholar 

  • Pageau, S.S., Gadi, K.S., Biggers, S.B. Jr. and Joseph, P.F. (1996). Standardized complex and logarithmic eigensolutions for n-material wedges and junctions. International Journal of Fracture 77, 51–76.

    Article  Google Scholar 

  • Seweryn, A. and Molski, K. (1996). Elastic stress singularities and corresponding generalized stress intensity factors for angular corners under various boundary conditions. Engineering Fracture Mechanics 55, 529–556.

    Article  Google Scholar 

  • Tada, H., Paris, P.C. and Irwin, G.R. (1973). The Stress Analysis of Cracks Handbook. Del Research Corporation, Hellertown.

    Google Scholar 

  • Tapponnier, P. and Brace, W.F. (1976). Development of stress-induced microcracks in Westerly granite. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstract 13, 103–112.

    Article  Google Scholar 

  • Theocaris, P.S. (1974). The order of singularity at a multi-wedge corner of a composite plate. International Journal of Engineering Science 12, 107–120.

    Article  MATH  Google Scholar 

  • Theocaris, P.S. and Panagiotopolous, P.D. (1992). On the consideration of unilateral contact and friction in cracks: the boundary integral method. International Journal for Numerical Methods in Engineering 35, 1697–1708.

    Article  MATH  ADS  Google Scholar 

  • Theocaris, P.S. and Panagiotopolous, P.D. (1993a). Crack-interfaces of fractal type with friction. Acta Mechamica 98, 63–78.

    Article  MATH  Google Scholar 

  • Theocaris, P.S. and Panagiotopolous, P.D. (1993b). Cracks of fractal geometry with unilateral contact and friction interface conditions. International Journal of Fracture 60, 293–310.

    Google Scholar 

  • Theocaris, P.S., Panagiotopolous, P.D. and Bisbos, C. (1993). Unilateral contact, friction and related interactions in cracks: the direct boundary integral method. International Journal of Solids and Structures 30, 1545–1561.

    Article  MATH  Google Scholar 

  • TheocarisP.S.MistakidisE.S.andPanagouliO.K.1992.FractalinterfaceswithunilateralcontactandfrictionconditionsComputerMethodsinAppliedMechanicsandEngineering 99 395–412.

  • Wang, Y.B. and Chau, K.T. (1997). A new boundary element method for plane elastic problems involving cracks and holes. International Journal of Fracture 87, 1–20.

    Article  MathSciNet  Google Scholar 

  • Wang, Y.B. and Chau, K.T. (1998). Analytic technique for mixed boundary value problems for plane elastic solids containing cracks and holes via boundary equations of complex variables. To be submitted.

  • Wang, Y.C., Hui, C.Y., Lagoudas, D. and Papadopoulos, J. (1991). Small-scale crack blunting at a bimaterial interface with Coulomb friction. International Journal of Fracture 52, 293–306.

    Google Scholar 

  • Williams, M.L. (1952). Stress singularities resulting from various boundary conditions in angular corner of plates in extension. Journal of Applied Mechanics ASME 19, 526–528.

    Google Scholar 

  • Williams, M.L. (1957). On the stress distribution at the base of a stationary crack. Journal of Applied Mechanics ASME 24, 109–114.

    MATH  Google Scholar 

  • Williams, M.L. (1959). The stresses around a fault or crack in dissimilar media. Bulletin of the Seismological Society of America 49, 199–204.

    MathSciNet  Google Scholar 

  • Wu, K.C., Chiu, Y.T. and Hwu, Z.H. (1992). A new boundary integral equation formulation for linear elastic solids. ASME Journal of Applied Mechanics 59, 344–348.

    Article  MATH  MathSciNet  Google Scholar 

  • Zhang, W.L. and Gudmundson, P. (1991). Frictional contact problems of kinked cracks modelled by the boundary integral method. International Journal for Numerical Methods in Engineering 31, 427–446.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil and Structural Engineering, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, China.

    K.T. Chau

  2. Department of Mechanics, Lanzhou University, Lanzhou, People's Republic of China

    Y.B. Wang

Authors
  1. K.T. Chau
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Y.B. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chau, K., Wang, Y. Singularity Analysis and Boundary Integral Equation Method for Frictional Crack Problems in Two-Dimensional Elasticity. International Journal of Fracture 90, 251–274 (1998). https://doi.org/10.1023/A:1007422305110

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1007422305110

Search

Navigation